Actualizado por ultima vez el 10 de mayo de 2022, por Luis Benites.
La I de Moran es una forma de medir la autocorrelación espacial.
En términos simples, es una forma de cuantificar qué tan cerca se agrupan los valores en un espacio 2-D. A menudo se usa en geografía y ciencia de la información geográfica (SIG) para medir qué tan cerca están agrupadas las diferentes características en un mapa, como los ingresos del hogar, el nivel de educación, etc.
Moran’s I: La fórmula
La fórmula para calcular el I de Moran es:
I = (N / W) * ΣΣw ij (x i – x ) (x j – x ) / Σ (x i – x ) 2
dónde:
- N: el número de unidades espaciales indexadas por i y j
- W: La suma de todos w ij
- x: La variable de interés (ingreso del hogar, años de escolaridad, etc.)
- x : la media de x
- w ij : una matriz de pesos espaciales
Es probable que nunca tenga que calcular esta medida a mano, ya que la mayoría del software estadístico puede calcularla por usted, pero es útil conocer la fórmula que se utiliza bajo el capó.
El valor de I de Moran puede variar de -1 a 1 donde:
- -1: La variable de interés está perfectamente dispersa
- 0: la variable de interés se dispersa aleatoriamente
- 1: la variable de interés está perfectamente agrupada
Junto con el cálculo de la I de Moran, la mayoría del software estadístico calculará un valor p correspondiente que se puede utilizar para determinar si los datos están dispersos aleatoriamente o no.
La prueba de Moran utiliza las siguientes hipótesis nulas y alternativas:
Hipótesis nula (H 0 ): los datos están dispersos al azar.
Hipótesis alternativa (H A ): Los datos no están dispersos al azar, es decir, están agrupados en patrones notables.
Si el valor p que corresponde al I de Moran es menor que un cierto nivel de significancia (es decir, α = .05), entonces podemos rechazar la hipótesis nula y concluir que los datos están agrupados espacialmente de tal manera que es poco probable que Han ocurrido solo por casualidad.
I de Moran: algunos ejemplos
Los siguientes ejemplos representan mapas falsos con diferentes valores para la I. de Moran.
Suponga que cada cuadrado del mapa representa un condado y que los condados con ingresos familiares promedio superiores a 50.000 dólares se muestran en azul.
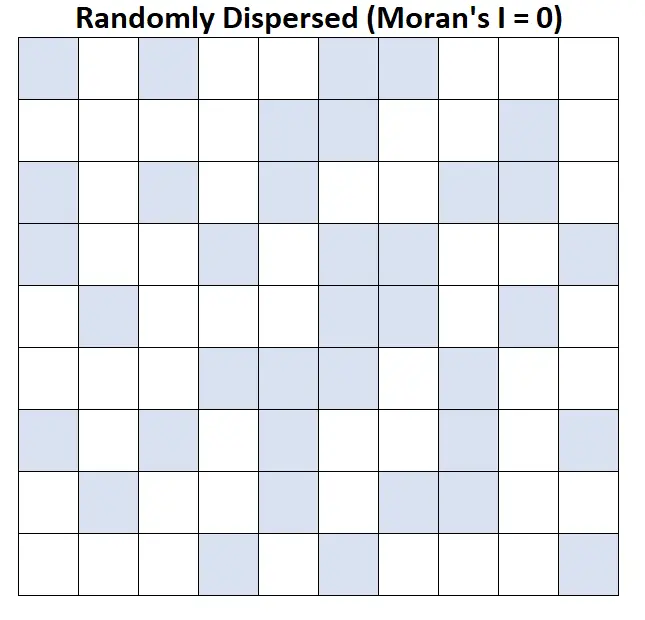
I de Moran = 0: el ingreso promedio de los hogares se distribuye aleatoriamente (es decir, grupos aleatorios en áreas aleatorias).
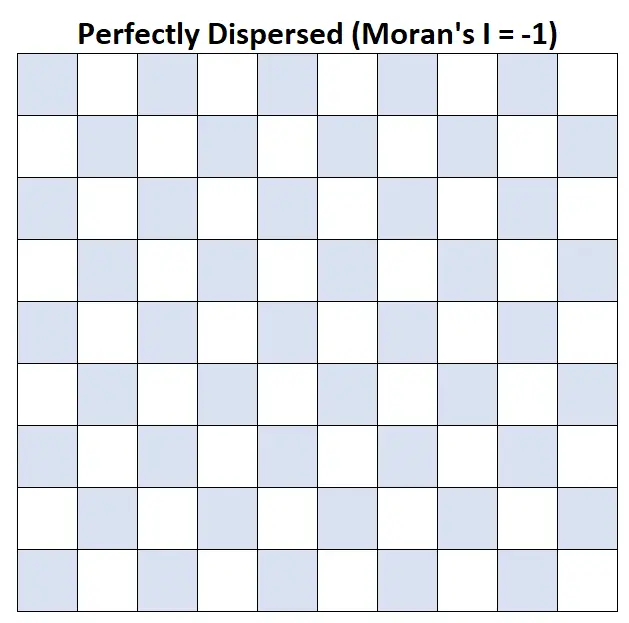
I de Moran = -1: El ingreso familiar promedio está perfectamente disperso.
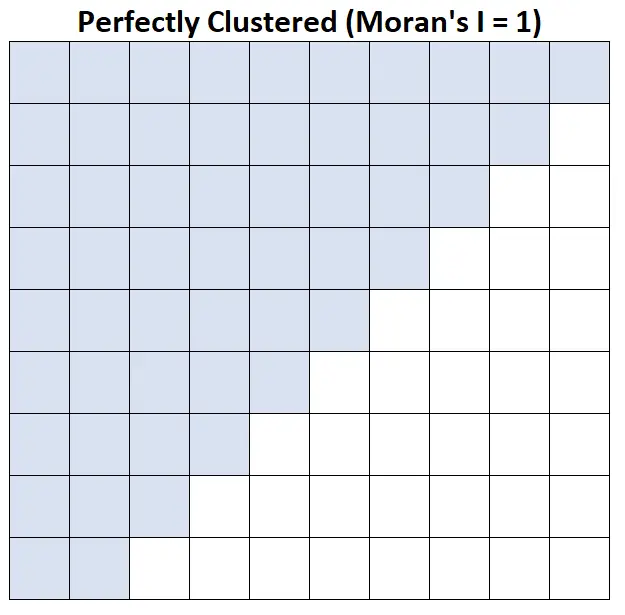
I = 1 de Moran: el ingreso familiar promedio está perfectamente agrupado.
Consulte este ejemplo para ver un ejemplo del mundo real de cómo calcular la I de Moran en el software estadístico R.
- https://r-project.org
- https://www.python.org/
- https://www.stata.com/
I’m a Bachelor of Economics gratuaded from the National University of San Agustin. I have experience in Python, R and other languages with aplications in Finance or Econometrics, I also have knowledge of statistics and econometrics. If you need help on some issues you can write to me.
