Propagación de errores (propagación de la incertidumbre)

Actualizado el 10 de febrero de 2022, por Luis Benites.

La propagación de errores (o propagación de la incertidumbre ) es lo que sucede con los errores de medición cuando usa esas mediciones inciertas para calcular otra cosa. Por ejemplo, puede usar la velocidad para calcular la energía cinética o puede usar la longitud para calcular el área. Cuando usa medidas inciertas para calcular otra cosa, se propagan (crecen mucho más rápido que la suma de los errores individuales). Para tener en cuenta esta propagación, utilice una de las siguientes fórmulas en sus experimentos.

Estas fórmulas asumen que sus errores son aleatorios y no están correlacionados (por ejemplo, si tiene errores sistemáticos, no puede usarlos).

1. Suma o resta

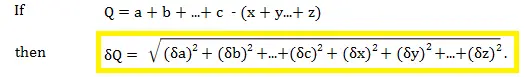
Fórmula aditiva para la propagación de errores.

Donde:

• a,b,c son medidas positivas
• x,y,z son medidas negativas
• δ es el error asociado con cada medición (el error absoluto ). δa es la incertidumbre asociada con la medición a, δb es la incertidumbre asociada con la medición b, y así sucesivamente.

Ejemplo de fórmula trabajada

Digamos que midió su altura (a) como 2,00 ± 0,03 m. Su pretina (b) está a 0,88 ± 0,04 m desde la parte superior de su cabeza, lo que significa que la longitud de su pantalón P sería p = H – w = 2,00 m – 0,88 m = 1,12 m.
La incertidumbre, utilizando la fórmula de la suma, es: Dando una medida final de 1,12 m ± 0,05 m.

2. Fórmula de multiplicación o división

Al calcular errores, no hay diferencia entre la multiplicación y la división.

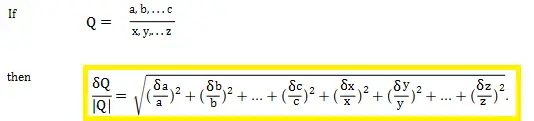
3. Fórmula de poder

Si n es un número exacto y Q = x ⁿ , entonces

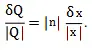
4. Fórmula de cantidad medida por número exacto

Si A es una medida exacta (por ejemplo, A = 9 o A = π) y Q = Ax, entonces:
δQ = |A| δx

5. Fórmula general para la Propagación de Errores

Quizás se pregunte por qué no puede simplemente sumar (o multiplicar o dividir) los errores y terminar con eso. ¿Por qué tenemos que usar fórmulas? Básicamente, un pequeño error de medición en una variable independiente , cuando se aplica a una función (digamos, una fórmula para el área, la energía cinética o la velocidad ) dará como resultado un error mucho mayor en la variable dependiente .

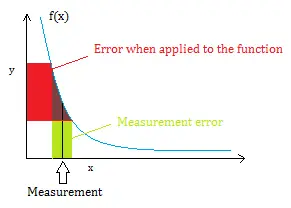
Propagación de errores en cálculo

Por qué las fórmulas funcionan requiere una comprensión del cálculo , y particularmente de las derivadas ; Se derivan de la ecuación de Gauss para errores normalmente distribuidos . Si tiene algún error en su medida (x), entonces el error resultante en la salida de la función (y) se basa en la pendiente de la línea (es decir, la derivada).
La fórmula general (utilizando derivadas) para la propagación de errores (de la que se derivan todas las demás fórmulas) es: Donde Q = Q(x) es cualquier función de x.

Las fórmulas de propagación de errores se basan en tomar derivadas parciales de una función con respecto a la variable con la incertidumbre. Digamos que tienes una función con tres variables (x, u, v) y dos de ellas (u, v) tienen incertidumbre. La varianza de x se puede aproximar por [1]:

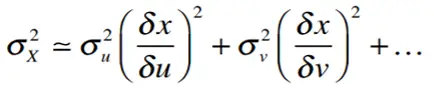
Ejemplo de pregunta : El volumen de gasolina entregado por una bomba es la diferencia entre las lecturas inicial (I) y final (F). Si cada lectura tiene una incertidumbre de ±0,02 ml, ¿cuál es el error en el volumen administrado?

Solución :

V = F – Yo; σ ² (V)
= σ ² (I) + σ ² (F)
= (0,02 ml) ² + (0,02 ml) ²
= 0,0008 ml ²
= 0,028 ml

El error en el volumen entregado es 0.028mL.

Este cálculo solo funcionará cuando las derivadas parciales sean 1. La fórmula cambia ligeramente cuando x es un producto (x = uv) o cociente (x = u/v):

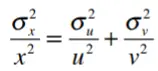
Ejemplo de pregunta n.º 2 : un contenedor de envío mide 12 x 10 x 8 pies con una incertidumbre de 0,1 pies. ¿Cuál es la incertidumbre en el volumen?

Paso 1: Calcular el volumen:
V = 12 x 10 x 8 = 960 pies ³ .

Paso 1: Trabaja la fórmula:
(0.1 pies) ² / (12 pies ² ) +
(0.1 pies) ² / (10 pies ² ) +
(0.1 pies) ² / (8 pies ² ) =
0.0.00145149572

Paso 3: Encuentre la variación de volumen (Paso 1 * Paso 2):
(0.00145149572)(960 pies ³ ) ² = 1337.698 pies ⁶

Paso 4: Saque la raíz cuadrada del Paso 3 para encontrar la incertidumbre en el volumen:
√(1337.698) = 36.57 pies ³ .

Referencias

10. Propagación de errores tutorial.doc. Recuperado el 14 de abril de 2021 de: https://foothill.edu/psme/daley/tutorials_files/10.%20Error%20Propagation.pdf