Actualizado por ultima vez el 30 de diciembre de 2021, por Luis Benites.
¿Qué es una prueba asintótica?
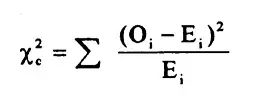
La prueba de chi-cuadrado es una prueba asintótica.
En la prueba de hipótesis , generalmente tiene dos opciones: una prueba exacta o una prueba asintótica . Puede pensar en una prueba asintótica como una aproximación y una prueba exacta como «el resultado exacto». Por ejemplo, la prueba de chi-cuadrado es una prueba asintótica; la versión exacta es la prueba binomial , que crea aproximaciones para los valores de p . Cuantos más puntos de datos tenga, mejor será la aproximación de la prueba asintótica. Sin embargo, las muestras grandes tienen un costo computacional: es posible que simplemente no tenga suficientes recursos informáticos para poder ejecutar una. En ese caso, una prueba exacta podría ser la mejor opción.
Como ejemplo específico, supongamos que desea probar la homogeneidad marginal con un tamaño de muestra de 6. La prueba habitual que se ejecuta es la prueba asintótica de McNemar . Sin embargo, la pequeña muestra significa que no puede usar la versión asintótica de la prueba de McNemars; En su lugar, puede utilizar la versión exacta, que utiliza probabilidades binomiales [1].
¿Por qué usar estadísticas de prueba asintótica?
A veces no es posible calcular estadísticas exactas para una prueba debido a restricciones de hardware o software. En cambio, podemos calcular una aproximación de la estadística «verdadera», un valor de prueba asintótico . Muchas pruebas estadísticas utilizaron valores de prueba asintóticos, especialmente para muestras grandes. Por ejemplo, es posible que vea un valor p informado como .001 cuando, de hecho, el valor p exacto puede tener docenas de lugares decimales.
Es computacionalmente eficiente dar estas aproximaciones y por lo general no hace ninguna diferencia en los resultados de una prueba estadística. Sin embargo, para muestras pequeñas o datos escasos, generalmente se recomiendan valores exactos, ya que las aproximaciones pueden ser significativamente diferentes de los valores reales.
Referencias
[1] Park, T. ¿Es la prueba exacta mejor que la prueba asintótica para probar la homogeneidad marginal? Recuperado el 17 de noviembre de 2021 de: https://www.stat.fi/isi99/proceedings/arkisto/varasto/park0373.pdf
Buenas!
Tengo una duda ¿A partir de qué tamaño muestral se consideraría más adecuado considerar la significación de la prueba asintótica como fiable? (>10?)