Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 12 de marzo de 2022, por Luis Benites.
¿Qué es una prueba binomial?
La prueba binomial se utiliza cuando un experimento tiene dos resultados posibles (es decir, éxito/fracaso) y tiene una idea de cuál es la probabilidad de éxito. Se ejecuta una prueba binomial para ver si los resultados de la prueba observados difieren de lo que se esperaba.
Ejemplo : teorizas que el 75% de los estudiantes de física son hombres. Encuesta una muestra aleatoria de 12 estudiantes de física y encuentra que 7 son hombres. ¿Sus resultados difieren significativamente de los resultados esperados?
Solución : use la fórmula binomial para encontrar la probabilidad de obtener sus resultados. La hipótesis nula de esta prueba es que sus resultados no difieren significativamente de lo esperado.
De los dos eventos posibles, desea encontrar el evento que le dio el resultado menos esperado . Esperaba 9 hombres (es decir, el 75% de 12), pero obtuvo 7, así que para este ejemplo resuelva para 7 o menos estudiantes. Nota : puedes encontrar un ejemplo paso a paso de cómo resolver la ecuación aquí en el artículo Fórmula binomial.
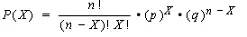
- p, la proporción observada, es 7/12, o 0,47.
- q, (1 – p) es 1 – .47.
- X es su número esperado de éxitos (75% de 12 es 9).
Reemplazando esos valores en la fórmula y resolviendo, obtienes:
0.158, que es la probabilidad de 7 o menos hombres de 12. Duplicando esto (para una prueba de dos colas ), da 0.315. Estos son sus valores p . Con muy pocas excepciones, siempre usará el valor duplicado.
Como el valor p de 0,315 es grande (asumo un nivel alfa del 5 % aquí, lo que significaría que los valores p de menos del 5 % serían significativos), no puede rechazar la hipótesis nula de que se esperan los resultados. En otras palabras, 7 no está fuera del rango de lo que esperarías.
Si, por el contrario, hubieras hecho la prueba con 4 hombres (p=.333 y q=.666), el valor de p duplicado hubiera sido .006, lo que significa que habrías rechazado el nulo.
Otra opción : usar una calculadora en línea, como esta: Calculadora binomial VassarStats.
Supuestos para la Prueba Binomial
- Los artículos son dicotómicos (es decir, hay dos) y nominales.
- El tamaño de la muestra es significativamente menor que el tamaño de la población.
- La muestra es una representación justa de la población.
- Los elementos de la muestra son independientes (un elemento no tiene relación con la probabilidad de otro).
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
