Actualizado por ultima vez el 12 de marzo de 2022, por Luis Benites.
La proporción muestral (p̂) describe la proporción de individuos en una muestra con una determinada característica o rasgo. Para encontrar la proporción de la muestra, divida el número de personas (o artículos) que tienen la característica de interés por el número total de personas (o artículos) en la muestra. Por ejemplo, supongamos que está realizando una encuesta a 100 personas preguntando si compran localmente o no. Si 35 personas dicen que compran localmente, entonces
p̂ puede tomar valores entre 0 y 1 (es decir, 0% a 100%).
Proporción muestral como variable aleatoria
La proporción muestral es una variable aleatoria porque varía aleatoriamente de una muestra a otra; si tuviera que encuestar a un conjunto diferente de 100 personas, podría obtener desde 0 respuestas positivas (es poco probable que las personas que viven en desiertos alimentarios compren localmente) hasta 100 (las personas en ciudades planificadas podrían no tener motivos para viajar para ir de compras). Cuando vemos la proporción de la muestra como una variable aleatoria, se denota con una P mayúscula: P̂.
Como esta estadística es una variable aleatoria, puede ser igual a la proporción de la población , o puede no serlo. Sin embargo, sus muestras se agruparán en torno a la verdadera proporción de la población; Si la verdadera proporción de personas que compran localmente es de 0,40, la proporción de la muestra se acercará a este número a medida que tome más y más muestras. Si tuviera el tiempo y el dinero para muestrear a todos, entonces p = p̂ = 0.40;. Entonces tiene sentido que la media de la proporción de la muestra sea igual a la proporción de la población.
Desviación estándar de la proporción de la muestra
Si toma muestras al azar muchas veces con un tamaño de muestra lo suficientemente grande, de modo que vea al menos cinco de cada resultado posible, la desviación estándar es igual a [1]:
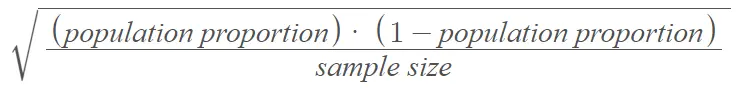
Si toma muchas muestras en las condiciones anteriores, el gráfico de la proporción de la muestra tendrá forma de campana. Más formalmente, decimos que la distribución muestral de la proporción muestral tiene una distribución aproximadamente normal .
Siguiente: Distribución muestral de la proporción muestral
Referencias
[1] Regla de proporciones muestrales. Recuperado el 4 de febrero de 2021 de: http://personal.psu.edu/drh20/016/fall2010/psu016confint.pdf
