Actualizado por ultima vez el 17 de agosto de 2021, por Luis Benites.
¿Qué es la regla de la probabilidad total?
La regla de probabilidad total (también llamada Ley de probabilidad total) divide los cálculos de probabilidad en partes distintas. Se usa para encontrar la probabilidad de un evento, A, cuando no se sabe lo suficiente sobre las probabilidades de A para calcularlo directamente. En cambio, toma un evento relacionado, B, y lo usa para calcular la probabilidad de A.
La probabilidad de a puede escribirse como la suma del evento B. La regla de la probabilidad total es:
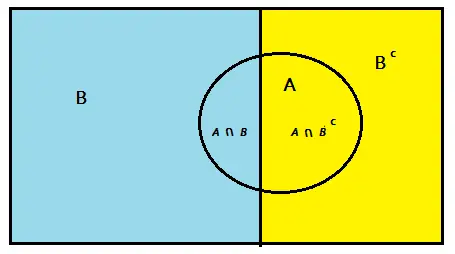
P(A) = P(A∩B) + P(A∩B c ).
Nota : ∩ significa “ intersección ” y B c es el complemento de B.
A veces, las probabilidades necesarias para el cálculo de la probabilidad total no se especifican de la manera exacta que necesita para resolver la ecuación. Una versión alternativa de la regla de probabilidad total (que se encuentra con la regla de la multiplicación) es:
P(A ∩ B) = P(A | B) * P(B) + P(A ∩ B c ) = P(A | B c )P(B c ).
En situaciones prácticas, puede ser difícil trabajar con estas ecuaciones. Es mucho más fácil trabajar con un árbol o una mesa.
¿ Necesita ayuda con una pregunta de tarea? ¡Mira nuestra página de tutoría!
Usando un árbol de probabilidad para encontrar la probabilidad total
Ejemplo de pregunta: el 80% de las personas acude regularmente a su médico de atención primaria; El 35% de esas personas sin problemas de salud surgen durante el año siguiente. Del 20% de las personas que no visitan a su médico regularmente, solo el 5% no tiene problemas de salud durante el año siguiente. ¿Cuál es la probabilidad de que una persona al azar no tenga problemas de salud en el año siguiente?
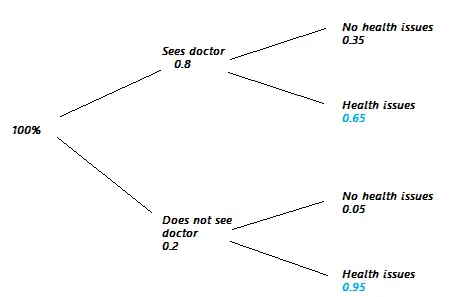
Paso 1: Dibuja un árbol. El siguiente árbol utiliza la información dada en la pregunta con la suma de dos probabilidades (en azul) obtenidas por el complemento . Por ejemplo, si el 5% de las personas no tienen problemas de salud, eso significa que el 95% de las personas sí tienen problemas de salud. Paso 2: Multiplica las probabilidades de cada rama. Por ejemplo, la rama superior tiene 0,8 en el primer segmento y 0,35 en el segundo. Estos cálculos se muestran en rojo en el siguiente gráfico:
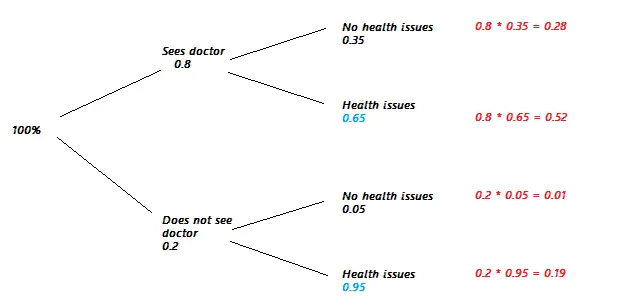
Paso 3: Encuentra las probabilidades que responden a la pregunta. Para este ejemplo, queremos la probabilidad de que una persona aleatoria no tenga problemas de salud. Si observa el gráfico, las ramas que conducen a «sin problemas de salud» son la rama superior y la tercera rama hacia abajo. Las probabilidades que aparecen en rojo son 0,28 y 0,01, por lo que la solución es:
0,28 + 0,01 = 0,29.
¡Eso es todo!
Usar una tabla para resolver la probabilidad total
La idea es la misma que la del árbol, solo que pones los datos en un formato de tabla. Esto es menos intuitivo que el árbol, aunque contiene la misma información. Esta primera tabla contiene la información dada en la pregunta: Tenga en cuenta que solo incluí en la tabla la información sobre «sin problemas de salud», ya que eso era lo que se preguntaba en la pregunta. Puede incluir toda la información (incluidas las personas que tuvieron problemas de salud), pero eso genera complicaciones en el siguiente paso (por lo tanto, es menos intuitivo que el árbol).

A continuación, las filas se multiplican para dar probabilidades conjuntas:

La regla de probabilidad total es la base del Teorema de Bayes .
Referencias
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.

