Actualizado por ultima vez el 17 de agosto de 2021, por Luis Benites.
Una constante de normalización garantiza que una función de densidad de probabilidad tenga una probabilidad de 1. La constante puede adoptar varias formas: podría ser un valor escalar , una ecuación o incluso una función . Como tal, no existe una constante de «talla única»; toda distribución de probabilidad que no sume 1 tendrá una constante de normalización individual.
En muchos casos, se conoce la función de densidad no normalizada, pero no la constante de normalización . En archivos PDF simples, la constante puede calcularse con relativa facilidad. En otros casos, especialmente cuando la constante es una función complicada del espacio de parámetros , puede ser imposible de calcular.
Ejemplos de constantes de normalización
En una distribución beta , la función en el denominador del pdf actúa como una constante de normalización.
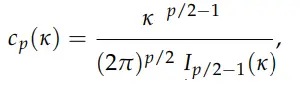
La constante de normalización de la distribución de Von Mises Fisher.
La constante de normalización en la distribución de Von Mises Fisher se encuentra integrando las coordenadas polares .
En la distribución de Kent , la constante de normalización es una ecuación:
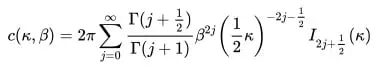
Para la regla de Bayes , escrita como [1]: El denominador es la constante de normalización que asegura que la distribución posterior suma 1; se puede calcular sumando el numerador sobre todos los valores posibles de la variable aleatoria . El cálculo de la normalización se vuelve mucho más difícil para procedimientos como la selección del modelo de factores bayesianos o el promedio del modelo bayesiano ; estos son notoriamente difíciles de calcular y generalmente involucran integrales de alta dimensión que son imposibles de resolver analíticamente [2].
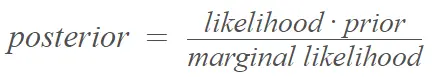
Referencias
[1] Murphy, K. En Símbolos. Recuperado el 16 de noviembre de 2021 de: https://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html[2] Gronau, Q. et al. Bridgesampling: un paquete R para estimar constantes de normalización. Recuperado el 16 de noviembre de 2021 de: https://cran.r-project.org/web/packages/bridgesampling/vignettes/bridgesampling_paper.pdf

