Contenido de este artículo
Actualizado el 16 de agosto de 2021, por Luis Benites.
Ver también: Superfactorial: Definición (Sloane, Pickover’s)
¿Qué es un factorial?
Mire el video para una definición y cómo calcular factoriales.
Factoriales! Ejemplos y simplificación Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
Los factoriales (!) son productos de todos los números enteros del 1 al n. En otras palabras, toma el número y multiplícalo hasta 1.
Por ejemplo:
- Si n es 3, entonces 3! es 3 x 2 x 1 = 6.
- Si n es 5, entonces 5! es 5 x 4 x 3 x 2 x 1 = 120.
Es una forma abreviada de escribir números. Por ejemplo, en lugar de escribir 479001600, ¡podrías escribir 12! en cambio (que es 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1).
¿Para qué se usa un factorial en las estadísticas?
En álgebra, probablemente te hayas encontrado con factoriales feos como (x – 10!)/(x + 9!). No te preocupes; No verás ninguno de estos en tu clase de estadísticas para principiantes. ¡Uf! La única vez que los verá es para problemas de permutación y combinación .
Las ecuaciones se ven así: Y eso es algo que puedes ingresar en tu calculadora (¡o en Google!).
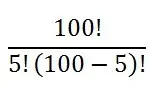
Artículo relacionado (de CalculusHowTo.com): ¿Por qué cero factorial es igual a uno?
Distribución factorial
Una distribución factorial ocurre cuando un conjunto de variables son eventos independientes . En otras palabras, las variables no interactúan en absoluto; Dados dos eventos x e y, la probabilidad de x no cambia cuando se factoriza y. Por tanto, la probabilidad de x, dado que ha pasado y —P(x|y)—, será igual a P(x).
La distribución factorial se puede escribir de muchas formas (Hinton, 2013; Olshausen, 2004):
- p(x,y) = p(x)p(y)
- p(x,y,z) = p(x)p(y)p(z)
- p(x 1 , x 2 , x 3 , x 4 ) = p(x 1 ) p(x 2 ) p(x 3 ) p(x 4 )
En el caso de un vector de probabilidad, el significado es exactamente el mismo. Es decir, un vector de probabilidad de una distribución factorial es el producto de las probabilidades de los términos individuales del vector.
Puede notar la falta del símbolo factorial (!) en cualquiera de las definiciones. Esto se debe a que la distribución se nombra porque las frecuencias sucesivas son cantidades factoriales, en lugar de que los términos sean factoriales en sí mismos.
Definición de una distribución factorial
Para una distribución factorial, P(x,y) = P(x)P(y). Podemos generalizar esto para más de dos variables (Olshausen, 2004) y escribir:
P(x 1 , x 2 ,…,x n ) = P(x 1 ) · P(x 2 · …· P(x n ).
Esta expresión también se puede escribir de manera más concisa como:
P(x 1 , x 2 ,…x n )= Π i P(x i ).
Ejemplos de distribución factorial
Nos gusta trabajar con distribuciones factoriales porque sus estadísticas son fáciles de calcular. En algunos campos, como la neurología, las situaciones mejor representadas por distribuciones de probabilidad complicadas e intratables se aproximan mediante distribuciones factoriales para aprovechar esta facilidad de manipulación.
Un ejemplo de una distribución factorial que se encuentra a menudo es la distribución normal generalizada p , representada por la ecuación
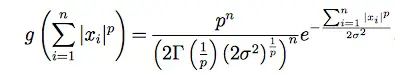
No entraré en el significado de esa fórmula aquí; si desea profundizar más, siéntase libre de leerlo aquí . Pero tenga en cuenta que cuando p = 2, esta es exactamente la distribución normal . Entonces la distribución normal también es factorial.
Función gamma
La función Gamma (a veces llamada función Gamma de Euler ) está relacionada con los factoriales mediante la siguiente fórmula:
Γ(n) = (x – 1)!.
En otras palabras, la función gamma es igual a la función factorial . Sin embargo, mientras que la función factorial solo se define para números enteros no negativos , la gamma puede manejar tanto fracciones como números complejos .
La función gamma multivariante (MGF) es una extensión de la función gamma para múltiples variables. Mientras que la función gamma solo puede manejar una entrada («x»), la versión multivariante puede manejar muchas. Suele definirse como:
Referencias
Abramowitz, M. y Stegun, IA (Eds.). “Función gamma (factorial)” y “Función gamma incompleta”. §6.1 y 6.5 en Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, novena edición . Nueva York: Dover, págs. 255-258 y 260-263, 1972.
Grötschel, M. et al. (Eds.) (2013). Optimización en línea de sistemas de gran escala . Springer Science & Business Media.
Hinton, G. (2013). Lección 1: Introducción al Aprendizaje Automático y Modelos Gráficos. Recuperado el 28 de diciembre de 2017 de: https://www.cs.toronto.edu/~hinton/csc2535/notes/lec1new.pdf
Jordan, I. et al. (2001). Modelos gráficos: fundamentos de la computación neuronal. Prensa del MIT.
Olshausen, B. (2004). Una cartilla de probabilidad. Recuperado el 27 de diciembre de 2017 de:
Obtenido de http://redwood.berkeley.edu/bruno/npb163/probability.pdf
Sinz, F. (2008). Caracterización de la p-Distribución Normal Generalizada. Recuperado el 27 de diciembre de 2017 de http://www.orga.cvss.cc/media/publications/SinzGerwinnBethge_2008.pdf el 27 de diciembre de 2017
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:

