Actualizado por ultima vez el 4 de noviembre de 2021, por Luis Benites.
Un vector de probabilidad es un vector (es decir, una matriz con una sola columna o fila) donde todas las entradas son no negativas y suman exactamente uno. A veces también se le llama vector estocástico .

Un vector de probabilidad puede representar probabilidades de sacar del 1 al 6.
Como ejemplo simple, el vector (1/6, 1/6, 1/6, 1/6, 1/6, 1/6) representa la distribución de probabilidad de una tirada aleatoria de un dado justo. Cada entrada representa sus posibilidades de tirar una cara de los dados (es decir, tiene una probabilidad de 1/6 de sacar 1, 2, 3, 4, 5 o 6).
No siempre es tan simétrico; de hecho, por lo general no lo es. Por ejemplo, el vector estocástico que representa la probabilidad de que llueva, nieve, esté nublado sin lluvia/nieve o esté soleado todo el día podría ser (0,5, 0, 0,40, 0,10). Tenga en cuenta que aquí las entradas aún suman uno, y las categorías representan todos los resultados posibles y no se superponen.
En esencia, un vector de probabilidad n -dimensional puede representar la distribución de probabilidad de un conjunto de n variables . Es una forma concisa y muy conveniente de representar la distribución de probabilidad de variables aleatorias discretas .
Propiedades del vector de probabilidad
Cada vector de probabilidad n-dimensional tiene una media de 1/n.
La longitud de un vector de probabilidad se calcula con la fórmula:
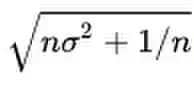 .
.
Aquí σ 2 es la varianza de todas las entradas en el vector de probabilidad. La ‘longitud’ de un vector de probabilidad, así definido, no tiene nada que ver con el número de entradas en la matriz.
- El vector de probabilidad más largo posible tiene el valor de 1 como una entrada y 0 en todas las demás. Tiene una longitud de 1. En una situación con cuatro alternativas posibles (como el ejemplo del clima anterior), el vector de probabilidad más largo posible sería {1000} (o {0100}, o {0010}, o {0001}).
- El vector de probabilidad más corto posible tiene 1/n como cada entrada, y su longitud es 1/ √(n). En el ejemplo de los dados con seis alternativas posibles, el vector más corto posible sería {1/n, 1/n, 1/n, 1/n, 1/n}.
Entonces, el vector más corto representa un sistema con certeza mínima (cualquiera de las opciones tiene la misma probabilidad de suceder) y el vector más largo representa un sistema con certeza máxima (usted sabe exactamente lo que sucederá). Por ejemplo, si el vector meteorológico es {1000}, entonces hay un 100 % de probabilidad de lluvia.
Si A es una matriz estocástica regular y es nxn, existe un único vector estocástico v para el cual Av = v.
Referencias
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Silva, G. (2007). Vect. de probabilidad, cadenas de Markov, matriz estocástica
Obtenido de https://www.dcce.ibilce.unesp.br/~gsilva/math152/Ch4-9-lay-classnotes.pdf el 11 de enero de 2018
Quinlan, R. (2006 ). Notas del curso MA203 Capítulo 4: Procesos de Markov
Obtenido de http://www.maths.nuigalway.ie/~rquinlan/MA203/section4-1.pdf el 11 de enero de 2018
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.

