Desigualdad de Cauchy-Schwarz: definición simple, ejemplo y prueba

Actualizado el 3 de enero de 2022, por Luis Benites.

¿Qué es la Desigualdad de Cauchy-Schwarz?

La Desigualdad de Cauchy-Schwarz (también llamada Desigualdad de Cauchy, Desigualdad de Cauchy-Bunyakovsky-Schwarz y Desigualdad de Schwarz) es útil para acotar valores esperados que son difíciles de calcular. Te permite dividir E[X ₁ , X ₂ ] en un límite superior con dos partes, una para cada variable aleatoria (Mukhopadhyay, 2000, p.149).

La fórmula es: Dado que X e Y tienen varianzas finitas .

Lo que esto básicamente quiere decir es que para dos variables aleatorias , X e Y, el valor esperado del cuadrado de ellas multiplicado por E(XY) ² siempre será menor o igual que el valor esperado del producto de los cuadrados de cada una. . E(X2 )E( ^Y2 ) ^.

Otras versiones

La desigualdad de Cauchy-Schwarz fue desarrollada por muchas personas durante un largo período de tiempo. Hizo su primera aparición en el trabajo de Cauchy de 1821 Cours d’analyse de l’Ecole Royal Polytechnique y fue desarrollado por Bunyakovsky (1859) y Schwarz (1888). Además de los diferentes nombres, también se puede expresar de varias maneras diferentes. Por ejemplo, la desigualdad se puede escribir, de manera equivalente, como:
Cov ² (X, Y) ≤ σ ² _x σ ² _y .

Hay otra versión de la desigualdad que reemplaza la expectativa E con integrales de tiempo . La fórmula es la misma, con la excepción de la expectativa/reemplazo integral:

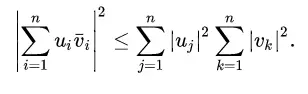
Aplicaciones

Podría decirse que la desigualdad de Cauchy-Schwarz es la desigualdad con el mayor número de aplicaciones. Además de probabilidad y estadística, la desigualdad se usa en muchas otras ramas de las matemáticas, que incluyen:

• Análisis clásico real y complejo ,
• Teoría de los espacios de Hilbert,
• Análisis numérico,
• Teoría cualitativa de ecuaciones diferenciales .

Ejemplo

Ejemplo de pregunta: use la desigualdad de Cauchy-Schwarz para encontrar el máximo de x + 2y + 3z,
dado que x ² + y ² + z ² = 1.

Sabemos que : (x + 2y + 3x) ² ≤ (1 ² + 2 ² 3 ² )(x ² + y ² + z ² ) = 14.

Por lo tanto : x + 2y + 3z ≤ √14.

La igualdad se cumple cuando : x/1 = y/2 = z/3.

Se nos da que : x ² + y ² + z ² = 1,
entonces:
x = 1/√14, x = 2/√14, x = 3/√14,

Pruebas

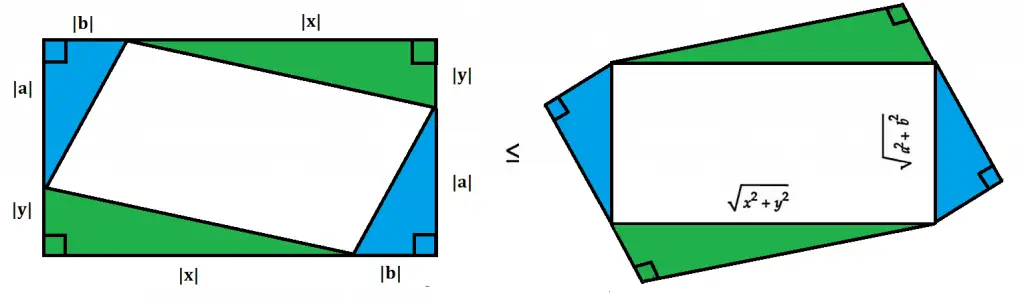
Esta es una de las pruebas más sencillas de visualizar. La siguiente “prueba sin palabras” es de Nelson (1994): Aquí hay otra prueba, esta vez, en palabras:

Suponga que E[X ² ]>0 y E[Y ² ]>0, y:

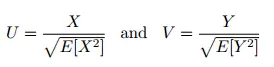
Se puede demostrar que : 2|UV| ≤ tu ² + V ² .

Por lo tanto : 2|E[UV] | ≤ 2E[|UV|] ≤ E[U ² ] + E[V ² ] = 2
Dando:
(E[UV]) ² ≤ (E[|UV|]) ² ≤ 1.

Esto implica que:
Puede encontrar una lista completa de pruebas (¡12 en total!) para la desigualdad de Cauchy-Schwarz en el artículo de Win & Wu ( PDF ).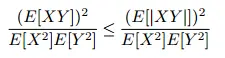

Referencias

Bunyakovsky (1859). Desigualdades, en Mémoires de l’Académie impériale des sciences de St. Pétersbourg. Recuperado el 7 de enero de 2018 de: https://www.biodiversitylibrary.org/bibliography/96968#/details.
Cauchy, A. (1821). Cours d’analyse de l’École royale polytechnique. Recuperado el 7 de enero de 2018 de: https://archive.org/details/coursdanalysede00caucgoog
Mukhopadhyay, N. (2000). Probabilidad e Inferencia Estadística . Prensa CRC.
Nelsen, R. (1994). Demostración sin palabras: Desigualdad de Cauchy-Schwarz, Matemáticas. Mag., 67, n. 1, pág. 20. Recuperado el 7 de enero de 2018 de: https://is.muni.cz/el/1441/podzim2013/MA2MP_SMR2/um/Nelsen–Proofs_without_Words.pdf
Schwarz, K. (1888). Uber ein die fl¨achen kleinsten fl¨achenhalts betreffendes problem der changesrechnung. Recuperado el 7 de enero de 2018 de: https://link.springer.com/chapter/10.1007%2F978-3-642-50665-9_11
Win, H. & Wu, S. (2000). Varias demostraciones de la desigualdad de Cauchy-Schwarz. Recuperado el 1 de enero de 2018 de: http://www.ajmaa.org/RGMIA/papers/v12e/Cauchy-Schwarzinequality.pdf