Distribuciones de probabilidad inusuales (de las que nunca has oído hablar)

Actualizado por ultima vez el 3 de enero de 2022, por Luis Benites.

Estas distribuciones de probabilidad inusuales (o nombres inusuales para distribuciones) nunca llegaron a la corriente principal. No los encontrará en sus libros de texto habituales, pero me encontré con esta interesante lista elaborada por el profesor Shakti [1].

Lista de distribuciones de probabilidad inusuales

1. La distribución de matriz se refiere a la distribución condicional de variables aleatorias independientes X ₁ (dado X ₂ , … ,X _n ).
2. La distribución de Arfwedsen (la distribución de recolección de cupones o copa Dixie) es una distribución de probabilidad discreta para un problema de muestreo de urnas para sorteos sin reemplazo. En concreto, aborda el problema “Una urna contiene N bolas numeradas. Hacemos n sorteos reemplazando la bola en la urna cada vez. ¿Cuál es la probabilidad de obtener v bolas diferentes?”[2]
3. Distribución agregada de binomios: el problema de agregar binomios se abordó brevemente en [3], haciendo referencia a una fórmula para un ideal tórico. De lo contrario, parece haber desaparecido en la oscuridad.
4. Distribución bipolar : un tipo específico de distribución bimodal que tiene dos picos distintos que ofrecen información contradictoria. En algunos casos, el término también puede referirse a la distribución bipolar de Watson.
5. La distribución de Bravais es otro nombre para la distribución normal bivariada (a veces también llamada distribución gaussiana bivariada o distribución bivariada de Laplace-Gauss).
6. Distribución de chi -barra cuadrada : una mezcla de distribuciones de chi-cuadrado , mezcladas en sus grados de libertad .
7. La distribución de Darmois-Koopman (o Koopman-Darmois) es un miembro de la clase de distribuciones de probabilidad de tipo exponencial .
8. La distribución de Moivre : otro nombre para la distribución normal . Se cree que el uso de «distribución de Moivre» para describir la distribución normal se originó con Freudenthal [4], quien abogó por el nombre porque De Moivre fue el primero en definir la distribución, en 1733 [5].
9. La distribución Elfving se define como La distribución lleva el nombre del estadístico y matemático finlandés Gustav Elfving (1908-1984), quien describió la distribución en 1947.
   
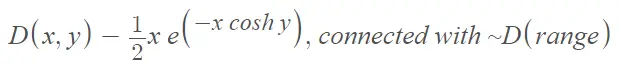
10. La función de distribución de excedencia (EDF) se define como 1 menos la función de distribución acumulativa (CDF) [1]:

    FED = 1 – CDF

Referencias

[1] Shakti, P. (2022). P-Distribución . Recuperado el 15 de marzo de 2022 de: https://p-distribution.com/probability-distributions-list/
[2] G. Arfwedson, Una distribución de probabilidad relacionada con los números de segunda clase de Stirling. Skand. Aktuaretidskr. 34 (1951), 121–132.
[3] Carlini, E. y Rapallo, F. (2013). Ideales tóricos con componentes lineales: una interpretación algebraica de agrupar las celdas de una tabla de contingencia .
[3] Freudenthal, H. (1966b). Waarschijnlijkheid en Statistiek [Probabilidad y estadística]. Haarlem: De Erven F.Bohn.
[4] Daw, R. & Pearson, E. Estudios de Historia de la Probabilidad y la Estadística. XXX. Derivación de la curva normal de 1733 de Abraham De Moivre: una nota bibliográfica. Biometrika vol. 59, No. 3 (diciembre de 1972), págs. 677-680 (4 páginas)
Oxford University Press