Probabilidad previa y posterior a la prueba

Actualizado el 3 de enero de 2022, por Luis Benites.

La probabilidad previa y posterior a la prueba se refiere a la probabilidad de tener una enfermedad antes de realizar una prueba de diagnóstico ( probabilidad previa a la prueba ) y después de realizar una prueba ( probabilidad posterior a la prueba ).

Cómo determinar la probabilidad previa y posterior a la prueba

Hay muchas formas diferentes de calcular la probabilidad previa y posterior a la prueba.

La probabilidad previa a la prueba es simplemente la prevalencia de la enfermedad en una población. La probabilidad previa a la prueba a veces se calcula mediante juicio clínico o datos disponibles (por ejemplo, datos de práctica). Una forma relativamente sencilla de encontrarlo en una población particular es calcular la probabilidad de que los pacientes tengan la enfermedad. Esto se puede lograr con la fórmula (Tape, nd):

P(D+) = ( Verdaderos positivos + Falsos negativos ) / (Verdaderos positivos + Falsos positivos + Verdaderos negativos + Falsos negativos)

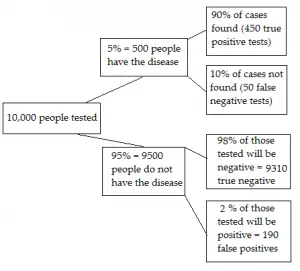
Se pueden usar falsos y verdaderos positivos/negativos para encontrar la probabilidad previa a la prueba.

Aplicar el teorema de Bayes es una opción para calcular probabilidades; la probabilidad posterior a la prueba depende no solo de la precisión de la prueba, sino también de la probabilidad de enfermedad previa a la prueba (Stoller & Michota, 2009), que en la terminología del teorema de Bayes se denomina probabilidad previa . Los valores predictivos se pueden utilizar para determinar la probabilidad previa y posterior a la prueba. Los valores predictivos se pueden calcular si conoce la sensibilidad y especificidad de la prueba y la probabilidad estimada de enfermedad previa a la prueba.

Ejemplo de probabilidad posterior a la prueba utilizando razones de verosimilitud

Un método alternativo es utilizar una razón de verosimilitud (LR), que combina sensibilidad y especificidad en un solo número (Fiebach & Barker, 2007). Este método es bastante sencillo (al menos, en comparación con el teorema de Bayes), pero debe seguir varios pasos. Parij et al. (2009) dan un ejemplo completo de cómo hacer esto. Los pasos se resumen a continuación:

1. Reúna su probabilidad previa a la prueba . Para este ejemplo, supongamos que es 2.5%.
2. Encuentre la sensibilidad y la especificidad de la prueba. Digamos que los datos publicados le dan una sensibilidad del 60 % y una especificidad del 97 %.
3. Calcular el LR. LR = Sensibilidad / 1- especificidad = 0,6 / 0,03 = 20
4. Calcule las probabilidades previas a la prueba usando la fórmula: Cuotas previas a la prueba = probabilidad previa a la prueba / (1 probabilidad previa a la prueba). Dando 0,025 / 0,975 = 0,03.
5. Encuentre las probabilidades posteriores a la prueba . Cuotas posteriores a la prueba = Cuotas previas a la prueba * LR = 0,03 * 20 = 0,6
6. Finalmente, calcule la probabilidad posterior a la prueba dividiendo las probabilidades posteriores a la prueba por las probabilidades posteriores a la prueba + 1: .6/ 1.6 = 0.375 o 37.5%.

Referencias

Fiebach, M. y Barker, L. (2007). Principios de Medicina Ambulatoria . Lippincott Williams & Wilkins.
Parikh, R. et al. (2009). Razones de verosimilitud: aplicación clínica en la práctica diaria . Indio J Ophthalmol.
Stoller, J. y Michota, F. (2009). The Cleveland Clinic Intensive Review of Internal Medicine Quinta edición . Lippincott Williams & Wilkins.
Tape, T. Conceptos Básicos y Definiciones. Recuperado el 4 de mayo de 2019 de: http://gim.unmc.edu/dxtests/reviewof.htm