Actualizado por ultima vez el 3 de enero de 2022, por Luis Benites.
¿Qué es el algoritmo de Boruvka?
El algoritmo de Boruvka es una forma de encontrar un árbol de expansión mínimo , un árbol de expansión donde se minimiza la suma de los pesos de los bordes. Fue el primer algoritmo desarrollado (en 1926) para encontrar MST; Otakar Boruvka lo usó para encontrar la ruta más eficiente para una red eléctrica.
Hay muchas formas de encontrar árboles de expansión mínimos. El algoritmo de Boruvka es un algoritmo codicioso y es similar al algoritmo de Kruskal y al algoritmo de Prim . Es básicamente un cruce entre los dos algoritmos. También se le conoce como algoritmo de Sollin , especialmente en informática.
Ejemplo del algoritmo de Boruvka
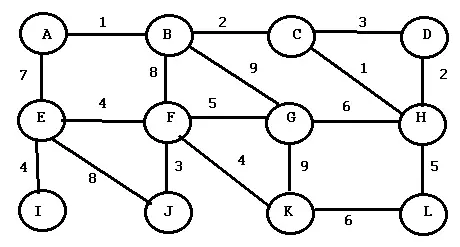
Encuentre el árbol de expansión mínimo para el siguiente gráfico usando el Algoritmo de Buruvka. Paso 1: Escriba una lista de componentes. Para este gráfico tenemos: A,B,C,D,E,F,G,H,I,J,K,L. Este paso es opcional pero le ayuda a realizar un seguimiento.
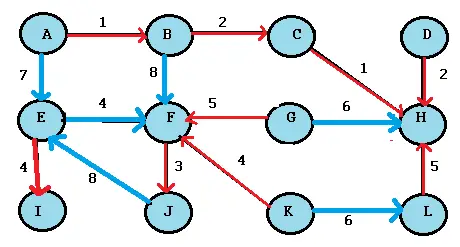
Paso 2: Resalte el borde saliente más barato para cada nodo en su lista. Por ejemplo, el nodo A tiene bordes salientes con pesos 1 y 7, por lo que resaltaremos 1. Continúe secuencialmente (para esta lista, vaya a B, luego a C…).
Directrices :
- En esta etapa, solo resalte un borde más barato para cada nodo.
- Para un empate (el nodo E tiene dos aristas con un peso de 4), asigne un peso menor a una de las aristas. Esto es arbitrario, pero debe permanecer constante durante todo el proceso. Para este ejemplo, haré que el borde de la izquierda tenga el peso más bajo.
- Resalte siempre el borde más barato, incluso si se ha resaltado antes . ¡No elija el borde con el siguiente peso más bajo! A efectos prácticos, esto significa que es posible que no tenga que resaltar nada para algunos nodos, si ya se ha resaltado el peso más bajo.
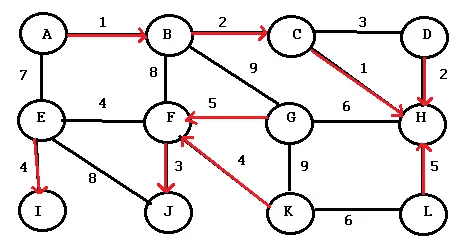
Paso 3: Resalte los grupos de árboles separados. Estos son los conjuntos de nodos conectados, a los que llamaremos componentes . Paso 4: Repita el algoritmo para cada componente (cada conjunto de color diferente). Esta vez, para cada nodo, elija el borde más barato fuera del componente . Por ejemplo, ABCDHL es un componente (nodos azules). Para el nodo A, el borde más barato fuera del componente es el nodo 7 (porque el nodo 1 está conectado dentro del componente). Estoy resaltando en azul para mayor claridad: puedes usar el color que quieras. Directrices :
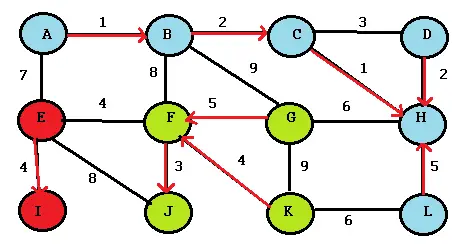
- Asegúrese de elegir el borde más barato fuera del componente. Para este gráfico y esta iteración, esos bordes están coloreados en negro.
- Como en la primera iteración, omita resaltar un borde si ya se ha resaltado esta vez.
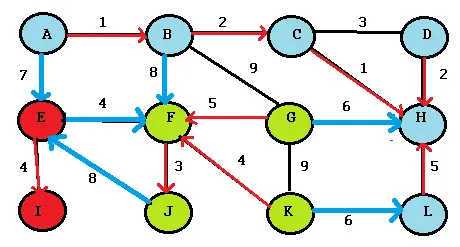
Paso 5: si todos sus nodos están conectados en un solo componente, ya está. Si no, repita el paso 4.
El siguiente gráfico muestra el MST final. He borrado los bordes no utilizados (negros).