Contenido de este artículo
Actualizado el 21 de diciembre de 2021, por Luis Benites.
¿Qué es un árbol de expansión mínimo?
Un árbol de expansión mínimo es un tipo especial de árbol que minimiza las longitudes (o «pesos») de los bordes del árbol. Un ejemplo es una compañía de cable que quiere tender línea a múltiples vecindarios; al minimizar la cantidad de cable tendido, la compañía de cable ahorrará dinero.
Un árbol tiene un camino que une dos vértices cualesquiera. Un árbol de expansión de un gráfico es un árbol que:
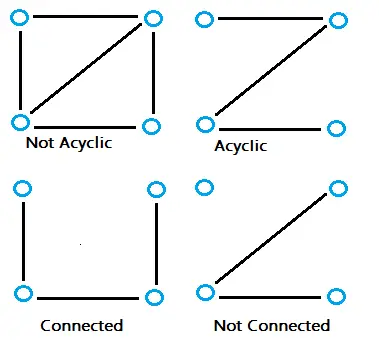
- Contiene todos los vértices del gráfico original.
- Alcanza (abarca) todos los vértices.
- es acíclico . En otras palabras, el gráfico no tiene ningún nodo que vuelva a sí mismo.
Incluso los gráficos más simples pueden contener muchos árboles de expansión. Por ejemplo, el siguiente gráfico:
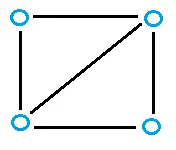
…tiene muchas posibilidades para los árboles de expansión, que incluyen:
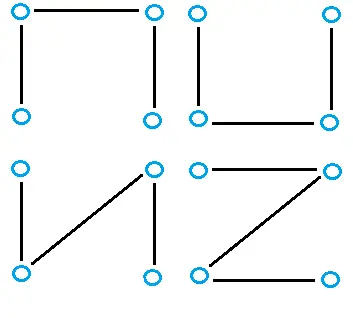
Encontrar árboles de expansión mínimos
Como probablemente puedas imaginar, los gráficos más grandes tienen más nodos y muchas más posibilidades para los subgráficos. La cantidad de subgráficos puede llegar rápidamente a millones o miles de millones, lo que hace que sea muy difícil (ya veces imposible) encontrar el árbol de expansión mínimo. Además, los largos suelen tener distintos pesos; a un borde de 5 m de largo se le puede dar un peso de 5, a otro de la misma longitud se le puede dar un peso de 7.
Algunos algoritmos populares para encontrar esta distancia mínima incluyen: el algoritmo de Kruskal, el algoritmo de Prim y el algoritmo de Boruvka . Estos funcionan para árboles de expansión simples. Para gráficos más complejos, probablemente necesitarás usar software.
Ejemplo del algoritmo de Kruskal
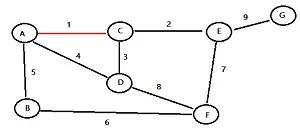
Encuentra el borde con el menor peso y resáltalo. Para este gráfico de ejemplo, he resaltado el borde superior (de A a C) en rojo. Tiene el peso más bajo (de 1): Encuentre el siguiente borde con el peso más bajo y resáltelo: Continúe seleccionando los bordes más bajos hasta que todos los nodos estén en el mismo árbol. Notas :
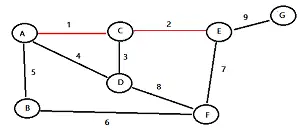
- Si tiene más de un borde con el mismo peso, elija un borde con el peso más bajo.
- Tenga cuidado de no completar un ciclo (enrutar un nodo de vuelta a sí mismo). Si su elección completa un ciclo, descarte su elección y pase al siguiente peso más grande.
El árbol de expansión mínimo terminado para este ejemplo se ve así:
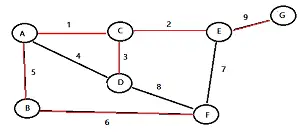
¿Qué es el algoritmo de Prim?
El algoritmo de Prim es una forma de encontrar un árbol de expansión mínimo (MST).
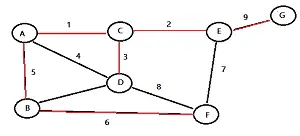
Un árbol de expansión mínima (mostrado en rojo) minimiza los bordes (pesos) de un árbol.
Cómo ejecutar el algoritmo de Prim
Paso 1: elige un nodo aleatorio y resáltalo. Para este ejemplo, elijo el nodo C. Paso 2: encuentre todos los bordes que van a los nodos no resaltados. Para este ejemplo, el nodo C tiene tres bordes con pesos 1, 2 y 3. Resalte el borde con el peso más bajo. Para este ejemplo, eso es 1. Paso 3: Resalte el nodo que acaba de alcanzar (en este ejemplo, ese es el nodo A).
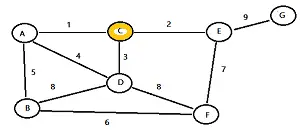
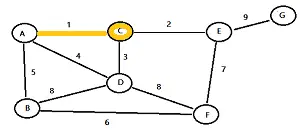
Paso 4: mire todos los nodos resaltados hasta ahora (en este ejemplo, son A y C). Resalte el borde con el peso más bajo (en este ejemplo, ese es el borde con peso 2). Nota : si tiene más de un borde con el mismo peso, elija uno al azar.
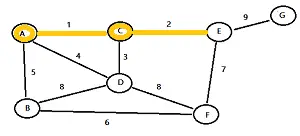
Paso 5: Resalte el nodo que acaba de alcanzar.
Paso 6: Resalte el borde con el peso más bajo. Elija entre todos los bordes que:
- Procede de todos los nodos resaltados.
- Llega a un nodo que aún no has resaltado
Paso 7: Repita los pasos 5 y 6 hasta que no tenga más nodos sin resaltar. Para este ejemplo en particular, los pasos específicos restantes son:
- una. Resalte el nodo E.
- b. Resalte el borde 3 y luego el nodo D.
- C. Resalte el borde 5 y luego el nodo B.
- d. Resalte el borde 6 y luego el nodo F.
- mi. Resalte el borde 9 y luego el nodo G.
- Análisis de conglomerados .
- Seguimiento y verificación de rostros en tiempo real (es decir, localización de rostros humanos en una transmisión de video).
- Protocolos en informática para evitar ciclos de red.
- Registro de imágenes basado en entropía .
- Rutas máximas de cuello de botella.
- Tramado (añadir ruido blanco a una grabación digital para reducir la distorsión).
El gráfico terminado se muestra en la parte inferior derecha de esta imagen:
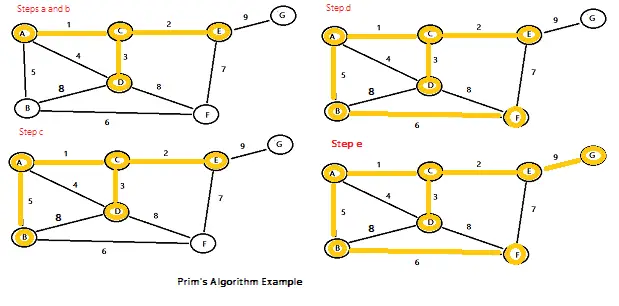
¡Eso es todo!
Aplicaciones de la vida real
Los árboles de expansión mínimos se utilizan para diseños de redes (es decir, redes telefónicas o de cable). También se utilizan para encontrar soluciones aproximadas para problemas matemáticos complejos como el problema del viajante de comercio . Otras aplicaciones diversas incluyen:
Referencias
Wu, B. y Chao, K. (2004). Árboles de expansión y problemas de optimización . Chapman y Hall/CRC.
¿Te hemos ayudado?
Deja un comentario en el muro del agradecimiento para que todos sepán que Statologos explica mejor y facil y si te es viable puedes hacer una donación:Puedes hacer un donativo
Muro del agradecimiento
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
