Actualizado por ultima vez el 21 de diciembre de 2021, por Luis Benites.
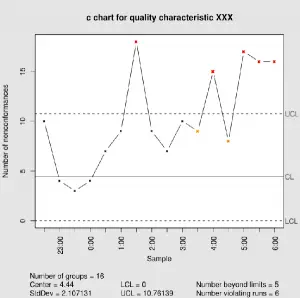
Un gráfico c es un tipo de gráfico de control que muestra cuántos defectos o no conformidades hay en muestras de tamaño constante, tomadas de un proceso (Misra, 2008).
fórmulas
Las fórmulas de la gráfica c son (Doty, 1996):
- Número de defectos por unidad c = Σc / Σn = Σc / m
- Límite de control superior (UCL) = c + 3√c
- Límite de control inferior (LCL) = c – 3√c
Donde:
- Σ es notación de suma ,
- n es el tamaño de la muestra,
- m es el número de subgrupos.
Gráfico U frente a gráfico C
Tanto la gráfica u como la gráfica c se utilizan para controlar defectos, y las dos gráficas difieren solo ligeramente; El gráfico c controla el número real de defectos por unidad, mientras que el gráfico u controla el número medio de defectos por unidad. Las fórmulas para crear los dos gráficos son idénticas, excepto que con el gráfico ac no es necesario dividir por el número total de elementos de la muestra, n .
Un gráfico c solo se puede usar si el tamaño de la muestra permanece constante. Si los tamaños de las muestras no son constantes, utilice el gráfico au en su lugar (Misra, 2008). Teóricamente, una gráfica p tampoco requiere un tamaño de muestra fijo, pero esas gráficas tienen un propósito diferente (las gráficas p muestran proporciones y solo se usan para la inspección de «aprobado/reprobado»).
Referencias
“Gráficas de Control de Conteos”. Manual de estadísticas de ingeniería de NIST/Sematech. Instituto Nacional de Normas y Tecnología. Consultado el 15 de junio de 2020.
Doty, L. Control estadístico de procesos . 1996. Prensa Industrial.
Misra, K. Manual de ingeniería de rendimiento , 2008. Springer.
Gráfico C de DanielPenfield / CC BY-SA (https://creativecommons.org/licenses/by-sa/3.0).
Montgomery, D. Introducción al Control Estadístico de Calidad. Hoboken, Nueva Jersey: John Wiley & Sons, Inc. pág. 289. ISBN 978-0-471-65631-9.
