Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 10 de febrero de 2022, por Luis Benites.
Hasta este punto de las estadísticas, probablemente haya estado trazando gráficos para un conjunto de números. Por ejemplo, podría haber graficado un conjunto de datos y encontrado que sigue la forma de una distribución normal con una puntuación media de 100. Donde las distribuciones de probabilidad difieren es que no está trabajando con un solo conjunto de números; está tratando con múltiples estadísticas para múltiples conjuntos de números . Si encuentra ese concepto difícil de comprender: no está solo.
Si bien la mayoría de las personas pueden imaginar cómo se ve el gráfico de un conjunto de números, es mucho más difícil imaginar cómo se ven las pilas de, por ejemplo, los promedios. Una explicación… Comencemos con una media, como las alturas de los estudiantes en la caricatura de arriba. Como probablemente sepa, las alturas (y muchos otros fenómenos naturales) siguen una forma de campana . Entonces, si encuestaras a tu clase, probablemente encontrarías algunas personas bajas, algunas personas altas y la mayoría de las personas estarían en el medio. digamos el promedio

la altura era 5’9″. Encuesta todas las clases de tu escuela y probablemente obtendrás un resultado cercano al promedio. Si tuviera 10 clases de estudiantes, podría obtener 5’9″, 5’8″, 5’10”, 5’9″, 5’7″, 5’9″, 5’9″, 5’10” , 5’7″ y 5’9″. Si graficas todos esos promedios, probablemente obtendrás un gráfico que se parece al «esporcaedro». Para otros conjuntos de datos, es posible que obtenga algo que parezca plano, como una distribución uniforme . Es casi imposible predecir cómo se verá ese gráfico, pero el teorema del límite central nos dice que si tiene una tonelada de datos, eventualmente se verá como una curva de campana. Esa es la idea básica: tomas tu promedio (u otra estadística, como la varianza) y trazas esas estadísticas en un gráfico.
Este video presenta el Teorema del Límite Central tal como se aplica a estas distribuciones. La «media de la distribución de muestreo de las medias» es solo lenguaje matemático para trazar un gráfico de promedios (como describí anteriormente) y luego encontrar el promedio de ese conjunto de datos.
media de la distribución muestral de la media Mira este video en YouTube .
Media de la distribución muestral de la media
En pocas palabras, esto es lo mismo que la media de la población . Por ejemplo, si la media de su población (μ) es 99, entonces la media de la distribución muestral de la media, μ m , también es 99 (siempre que tenga un tamaño de muestra lo suficientemente grande). Si quieres entender por qué , mira el video o lee a continuación.
media de la distribución muestral de la media Mira este video en YouTube .
El teorema del límite central.
En términos generales, el teorema del límite central nos dice que si tenemos un gran número de variables independientes distribuidas de manera idéntica , la distribución seguirá aproximadamente una distribución normal . No importa cuál sea la distribución subyacente.
Aquí hay un ejemplo simple de la teoría: cuando lanzas un solo dado, tus probabilidades de obtener cualquier número (1, 2, 3, 4, 5 o 6) son las mismas (1/6). La media de cualquier tirada es (1 + 2 + 3 + 4 + 5 + 6) / 6 = 3,5. Los resultados de una tirada de un dado se muestran en la primera figura a continuación: parece una distribución uniforme . Sin embargo, a medida que aumenta el tamaño de la muestra (dos dados, tres dados…), la distribución de la media se parece cada vez más a una distribución normal. Eso es lo que predice el teorema del límite central.
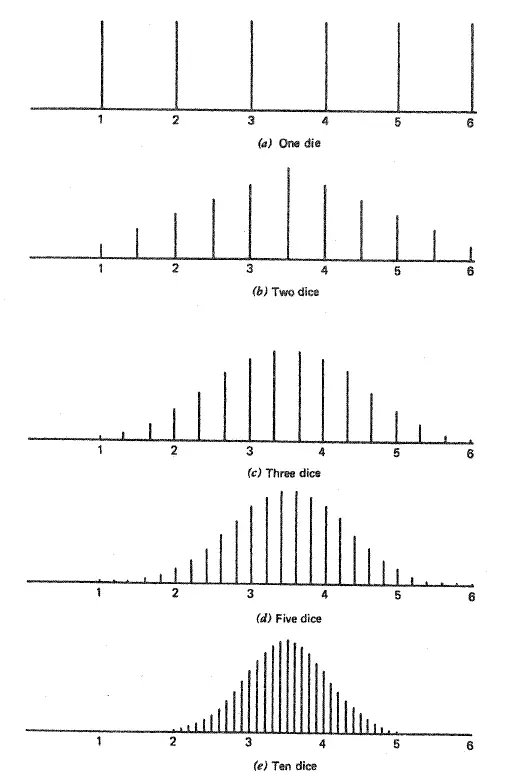
Imagen: Universidad de Michigan.
A medida que aumenta el tamaño de la muestra, la distribución de la media se acercará a la media poblacional de μ y la varianza se acercará a σ 2 /N, donde N es el tamaño de la muestra.
Puede pensar en una distribución de muestreo como una distribución de frecuencia relativa con una gran cantidad de muestras.
La media de la distribución muestral de la fórmula media
La fórmula es μ M = μ, donde μ M es la media de la distribución muestral de la media.
Media de Muestreo Distribución de la Proporción
La media de la distribución muestral de la proporción, P, es un caso especial de la distribución muestral de la media. La media de la distribución muestral de la proporción está relacionada con la distribución binomial .
Una distribución binomial está relacionada con la distribución media de muestreo de la proporción.
Las proporciones son algo que probablemente ya sepas. Por ejemplo: se pregunta a 100 personas si son demócratas. Si 50 personas responden “sí”, entonces la proporción muestral p = 50/100. Técnicamente (la «manera matemática»): una proporción de muestra es donde se toma una muestra aleatoria de objetos n de una población P; si x objetos tienen una determinada característica entonces la proporción muestral “p” es: p = x/n.
La distribución muestral de una proporción es cuando repites tu encuesta o sondeo para todas las muestras posibles de la población. Por ejemplo: en lugar de preguntar a 1000 dueños de gatos qué comida para gatos prefiere su mascota, puede repetir la encuesta varias veces.
Media de Muestreo Distribución de la Proporción
Si se toma una muestra aleatoria de n observaciones de una población binomial con parámetro p, la distribución muestral (es decir, todas las muestras posibles tomadas de la población) tendrá una media u p =p. Con una muestra grande, la distribución muestral de una proporción tendrá una distribución normal aproximada .
Desviación estándar de la distribución muestral de la proporción
La desviación estándar de la distribución muestral de la proporción, P, también está estrechamente relacionada con la distribución binomial y es un caso especial de distribución muestral.
Ejemplo : realiza una encuesta sobre los puntajes GRE de los estudiantes universitarios y calcula que la desviación estándar es 1. Es muy poco probable que obtenga los mismos resultados si repite la encuesta (puede obtener 1.1, 1.2 o 0.9). Por lo tanto, querrá repetir la encuesta la mayor cantidad de veces posible (es decir, extraiga todas las muestras posibles de tamaño n de la población). Tendrá un rango de desviaciones estándar, una para cada muestra.
Distribución de muestreo de una proporción
Aquí es cuando repite su encuesta para todas las muestras posibles de la población. Por ejemplo: en lugar de encuestar a 100 personas una vez para preguntarles si son demócratas, las encuestará varias veces para obtener una mejor estimación de su estadística.
Desviación Estándar
Si se toma una muestra aleatoria de n observaciones de una población binomial con parámetro p, la distribución muestral (es decir, todas las muestras posibles tomadas de la población) tendrá una desviación estándar de:
Desviación estándar de la distribución binomial = σ p = √[pq/n] donde q=1-p.
Cuando la muestra es grande, la distribución tendrá una distribución normal aproximada .
¡ Visite nuestro canal de YouTube para obtener más consejos y ayuda para las estadísticas!
Referencias
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Levine, D. (2014). Incluso usted puede aprender estadísticas y análisis: una guía fácil de entender sobre estadísticas y análisis, 3.ª edición. Prensa Pearson FT
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
