Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 15 de septiembre de 2021, por Luis Benites.
Fórmula de distribución hipergeométrica
Mira el video para ver un ejemplo:
Ejemplo de fórmula de distribución hipergeométrica Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
La definición (algo formal) de la distribución hipergeométrica, donde X es una variable aleatoria, es: Donde:
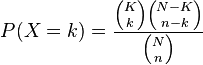
- K es el número de éxitos en la población
- k es el número de éxitos observados
- N es el tamaño de la población
- n es el número de sorteos
Podría simplemente conectar sus valores en la fórmula . Sin embargo, si las fórmulas no son lo tuyo, otra forma es simplemente pensar en el problema, usando tu conocimiento de las combinaciones.
Distribución Hipergeométrica Ejemplo 1
Una baraja de cartas contiene 20 cartas: 6 cartas rojas y 14 cartas negras. Se extraen 5 cartas al azar sin reemplazo . ¿Cuál es la probabilidad de sacar exactamente 4 tarjetas rojas?
La probabilidad de elegir exactamente 4 tarjetas rojas es:
P(4 tarjetas rojas) = # muestras con 4 tarjetas rojas y 1 tarjeta negra / # de muestras posibles de 4 tarjetas
Usando la fórmula de combinaciones, el problema se convierte en: En resumen, la fórmula anterior se puede escribir como: (6C4*14C1)/20C5 donde
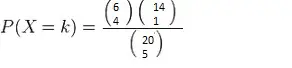
- 6C4 significa que de 6 tarjetas rojas posibles, estamos eligiendo 4.
- 14C1 significa que de 14 cartas negras posibles, estamos eligiendo 1.
Solución = (6C4*14C1)/20C5 = 15*14/15504 = 0,0135
La distribución binomial no se aplica aquí, porque las cartas no se reemplazan una vez que se extraen. En otras palabras, los juicios no son eventos independientes. Por ejemplo, para 1 tarjeta roja, la probabilidad es 6/20 en el primer sorteo. Si esa tarjeta es roja, la probabilidad de elegir otra tarjeta roja cae a 5/19.
Distribución Hipergeométrica Ejemplo 2
Un distrito electoral pequeño tiene 101 votantes mujeres y 95 votantes hombres. Se extrae una muestra aleatoria de 10 votantes. ¿Cuál es la probabilidad de que exactamente 7 de los votantes sean mujeres?
101C7*95C3/(196C10)= (17199613200*138415)/18257282924056176 = 0,130
Donde:
- 101C7 es el número de formas de elegir 7 hembras de 101 y
- 95C3 es el número de formas de elegir 3 votantes masculinos* de 95
- 196C10 es el total de votantes (196) de los cuales estamos eligiendo 10
*Eso es porque si 7/10 votantes son mujeres, entonces 3/10 votantes deben ser hombres.
¡ Visite nuestro canal de YouTube para ver cientos de videos de ayuda sobre estadísticas!
Aplicación de la Distribución Hipergeométrica en la Vida Real: Ejemplos
La distribución hipergeométrica describe el número de éxitos en una secuencia de n ensayos de una población finita sin reemplazo. A primera vista, puede parecer que se trata de una distribución puramente académica, pero en realidad existen muchas aplicaciones diferentes de la distribución hipergeométrica en la vida real.
 Una de las aplicaciones más comunes de la distribución hipergeométrica es el control de calidad industrial, como el cálculo de probabilidades de piezas defectuosas producidas en una fábrica. Digamos que una línea de fábrica produce 1% de piezas defectuosas que se empaquetan al final de la línea; La distribución hipergeométrica se puede utilizar para modelar la aparición de piezas defectuosas con fines de control de calidad, siempre que no se reemplacen los elementos que se toman como muestra de una caja.
Una de las aplicaciones más comunes de la distribución hipergeométrica es el control de calidad industrial, como el cálculo de probabilidades de piezas defectuosas producidas en una fábrica. Digamos que una línea de fábrica produce 1% de piezas defectuosas que se empaquetan al final de la línea; La distribución hipergeométrica se puede utilizar para modelar la aparición de piezas defectuosas con fines de control de calidad, siempre que no se reemplacen los elementos que se toman como muestra de una caja.
En electroquímica , la distribución hipergeométrica puede predecir el efecto del deterioro de la superficie sobre el comportamiento de los electrodos para cualquier proceso de electrodos con dos reacciones en competencia. Esto brinda información valiosa sobre la efectividad de las interfaces electrodo-electrolito y mejora la interpretación de las mediciones de las propiedades de la superficie [1].
Si juegas al póquer , la distribución hipergeométrica puede indicarte la probabilidad de obtener 3 del mismo palo en una mano de 5 cartas (o cualquier número de otras combinaciones de cartas y manos).
El juego de lotería PowerBall es un sorteo televisado de dos partes. En la primera etapa, se extraen al azar cinco bolas blancas de un tazón de 49 bolas. En la segunda etapa, se extrae al azar una bola roja (la PowerBall) de un tazón de 42 bolas. La probabilidad de éxito cambia de un sorteo a otro (las bolas no se reemplazan), por lo que las probabilidades del juego se pueden modelar con la distribución hipergeométrica [2].
Referencias
[1] Fahidy, T. (2012). Una aplicación de la teoría de la distribución hipergeométrica a los procesos competitivos en el deterioro de las superficies de los electrodos. En Comunicaciones electroquímicas, 282-284.[2] Anderson, J. y Schmidt, J. (2002). ¿Jugando Powerball? . Actas. Jornada Anual de Tributación y Acta de la Asamblea Anual de la Asociación Tributaria Nacional. págs. 377-382.
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Klein, G. (2013). La caricatura Introducción a la estadística. Colina y Wamg.
Lindström, D. (2010). Schaum’s Easy Outline of Statistics , segunda edición (Schaum’s Easy Outlines) 2ª edición. Educación McGraw-Hill
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
