Actualizado por ultima vez el 28 de abril de 2022, por Luis Benites.
¿Qué es el estimador de James-Stein?
Es común en las estadísticas tomar promedios para hacer predicciones. Por ejemplo, la media de la muestra (la puntuación media de todas las muestras) se utiliza como estimador de la media de la población . Los estimadores de James-Stein mejoran estos promedios reduciéndolos a un promedio más central. La técnica lleva el nombre de Charles Stein y Willard James, quienes simplificaron el método original de Stein de 1956.
Cálculos
Los pasos básicos son:
- Calcule la media muestral (X̄).
- “Reducir” las puntuaciones individuales hacia (X̄); Reduzca los valores más grandes y aumente los valores más pequeños. Cada uno de estos valores reducidos individuales es un estimador de James-Stein, z.
La fórmula básica para el estimador de James-Stein es:
z = x̄ + c(y – x̄)
Donde:
- (y – x̄) = diferencia entre una puntuación individual y la media de la muestra,
- c = un factor de contracción.
Existen otras fórmulas, pero todas tienen en común el factor de reducción. Por ejemplo, en lugar de la media de la muestra, podría utilizar la media de una distribución anterior ( m ). En ese caso, ȳ podría reemplazarse por m . El valor del factor de contracción se calcula después de recopilar los datos de la muestra y viene dado por la fórmula: Donde:
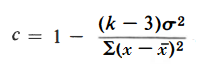
- x = valores individuales,
- x̄ = media muestral,
- k = número de medias desconocidas (debe ser 2 o más),
- σ 2 = varianza .
El valor del factor de reducción debe ser inferior a 1. Por ejemplo, un valor de 0,3 reduciría los valores en aproximadamente un 70 por ciento.
Estimadores de James-Stein frente a medias muestrales
El estimador de James-Stein es una desviación significativa de la escuela de pensamiento «tradicional» que establece que la media de la muestra es el mejor estimador de la media de la población. Stein y James demostraron que existe un mejor estimador que el estimador «perfecto», lo que parece ser una especie de paradoja. Sin embargo, el estimador de James-Stein supera la media muestral cuando hay varias medias poblacionales desconocidas, no solo una. Los medios no tienen que estar relacionados, por lo que deben elegirse cuidadosamente. La combinación de medios completamente no relacionados le dará un resultado, pero no tendrá sentido. Bradley Efron y Carl Morris (1977) ofrecen el ejemplo extremo de combinar promedios de bateo en béisbol y proporciones de autos importados; Puede calcular una media para estos, pero no tendrá ningún sentido.
Referencias
Efron, B. y Morris, C. (1977), «La paradoja de Stein en estadística». Científico americano. 236 (5): 119–127
James, W. y Stein, C., (1961). «Estimación con pérdida cuadrática». Actas del Cuarto Simposio de Berkeley, vol. 1 (Berkeley, California: University of California Press), págs. 361-379.
Stein C. (1956). “Inadmisibilidad del estimador habitual para la media de una distribución normal multivariante ”. Actas del Tercer Simposio de Berkeley sobre Estadística Matemática y Probabilidad. vol. 1. Prensa de la Universidad de California; Berkeley, CA, EE. UU.: págs. 197–208

