Actualizado por ultima vez el 28 de abril de 2022, por Luis Benites.
El Triángulo de Pascal es un patrón numérico en forma de (¡no es sorprendente!) un triángulo. Lleva el nombre del matemático francés Blaise Pascal. El Triángulo de Pascal tiene muchas aplicaciones en matemáticas y estadísticas, incluida su capacidad para ayudarlo a calcular combinaciones .
Fila 0 1 Fila 1 1 1 Fila 2 1 2 1 Fila 3 1 3 3 1 Fila 4 1 4 6 4 1 Fila 5 1 5 10 10 5 1 Fila 6 1 6 15 20 15 6 1 Fila 7 1 7 21 35 35 21 7 1
Cada número en el triángulo es la suma de los dos números que están arriba. Por ejemplo, hay una
en el centro de la fila 4: es la suma de 3 y 3 en la fila de arriba. El primer y último número de cualquier fila siempre será 1.
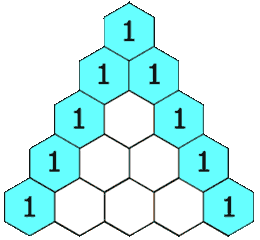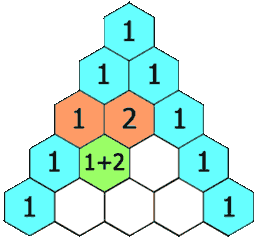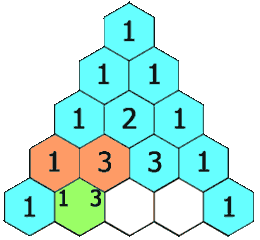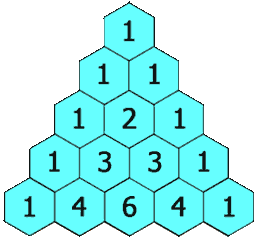
Triángulo de Pascal Imagen: Hersfold | Wikimedia Commons.
Cómo encontrar combinaciones con el Triángulo de Pascal
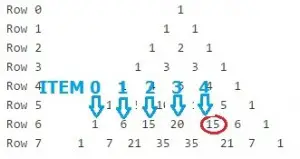
El Triángulo de Pascal se puede utilizar para encontrar combinaciones. La fila superior en el Triángulo de Pascal es la fila cero, y el primer elemento de cualquier fila (los 1) son el elemento cero en esa fila. Por ejemplo, supongamos que queríamos encontrar 6_C_4. Mire en la Fila 6, el artículo número 4. La respuesta es 15.
Otros usos
Fuera de la probabilidad , el Triángulo de Pascal también se usa para:
- Álgebra, donde se puede usar el coeficiente de polinomios para encontrar los números en el triángulo de Pascal. Álgebra está fuera del alcance de este sitio, pero puede encontrar una excelente explicación de este concepto en el sitio web de Dr. Math .
- Encontrar números triangulares (1, 3, 6, 10, 15, 21, 28, 36, 45, …). Los números triangulares son los “puntos” que forman un triángulo. Por ejemplo, puede hacer un triángulo muy simple a partir de 3 puntos, uno en cada ángulo de esquina. Para obtener más información sobre los números triangulares, consulte Math is Fun .
Hay muchos, muchos otros patrones interesantes que puedes encontrar en el triángulo, incluidos los números primos, los números catalanes y la secuencia de Fibonacci. La página de J Wilson en el sitio web de la Universidad de Georgia tiene un excelente resumen de muchos patrones numéricos que están ocultos en el Triángulo de Pascal.
¡ Visite nuestro canal de YouTube para ver cientos de videos de ayuda sobre estadísticas!

