Función de distribución de probabilidad: Definición, TI83 NormalPDF

Actualizado el 25 de abril de 2022, por Luis Benites.

Las variables continuas pueden asumir un número infinito de variables . Por ejemplo, podría tener una variable aleatoria Y que represente posibles pesos:

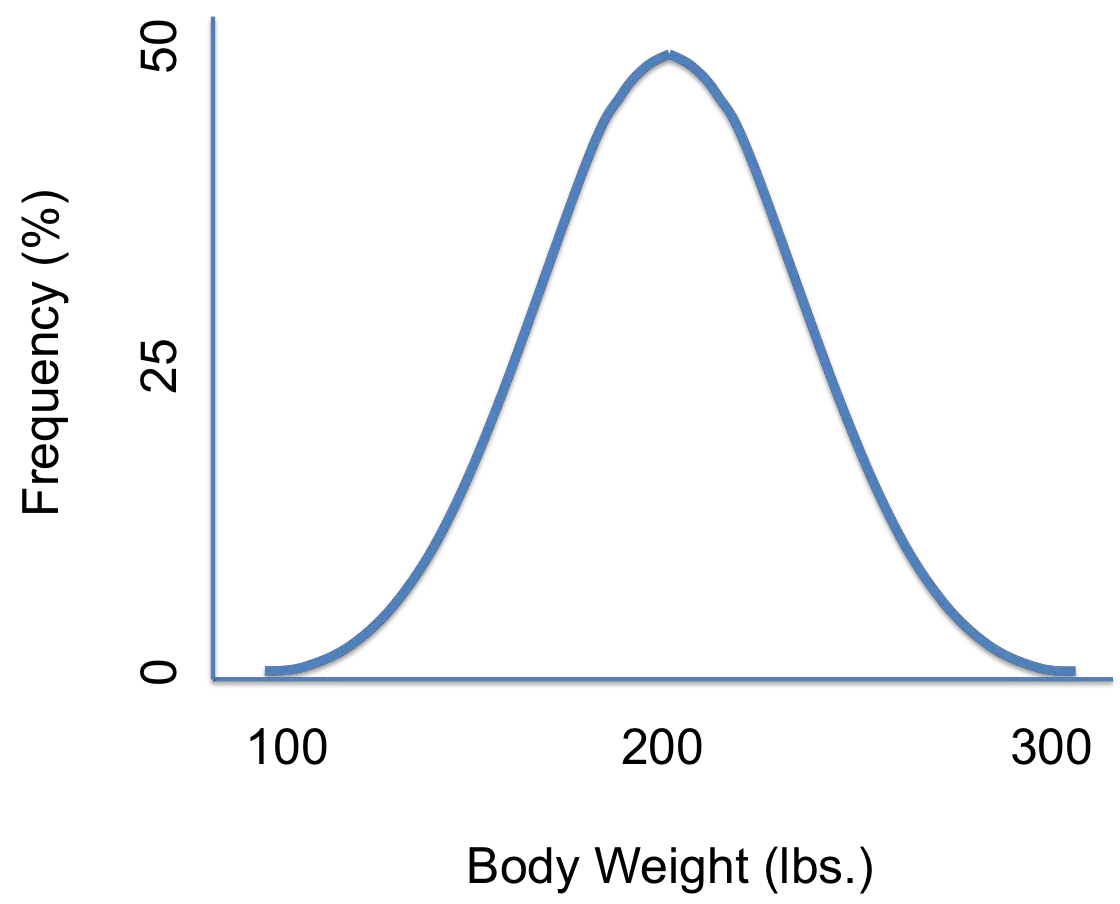
La función de distribución de probabilidad que se muestra arriba muestra todos los valores posibles para Y, que para este caso tiene una cantidad infinita de posibilidades. Por ejemplo, la variable aleatoria Y podría ser igual a 180 libras, 151,2 libras o 201,9999999999 libras.

Podemos usar funciones de distribución de probabilidad para responder una pregunta como:
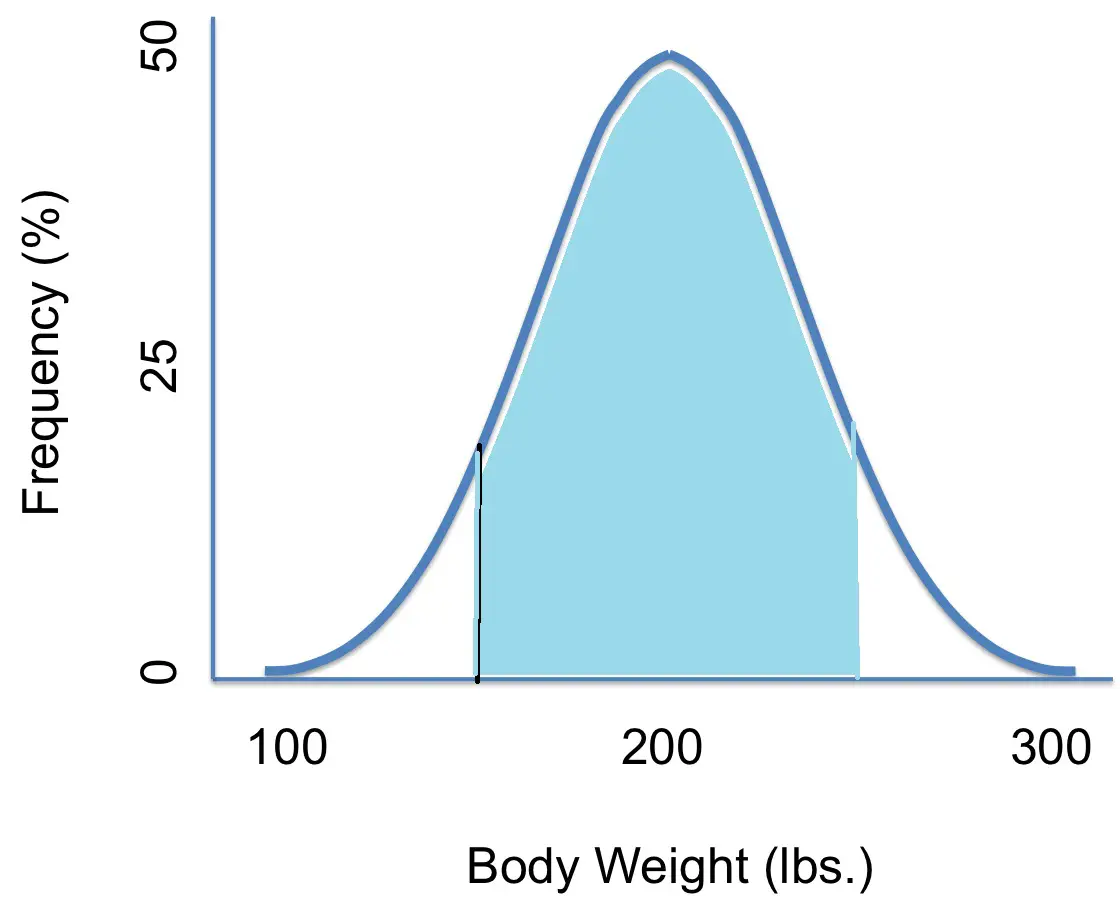
¿Cuál es la probabilidad de que una persona pese entre 150 y 250 libras?
Escrita en notación, la pregunta se convierte en:
P(150 < Y < 250)
Para responder la pregunta, sombrea el área en el gráfico: luego aproxima el área. Mirando el área sombreada, parece que es alrededor del 75 por ciento. Entonces, P(150 < Y < 250) = 75%.

Puede usar la misma técnica para calcular la probabilidad de que sea menor o mayor que cierto número. Simplemente sombree el área a la derecha del número (para mayor que) o a la izquierda del número (para menor que).

¡Tenga cuidado al leer los gráficos de funciones de distribución de probabilidad!

Las funciones de probabilidad son excelentes para calcular intervalos (porque entonces tienes un área para medir). Sin embargo, debe tener un poco de precaución al leer los gráficos de función de distribución de probabilidad, especialmente cuando se trata de números exactos. Por ejemplo: ¿Qué pasa con la probabilidad de que una persona pese exactamente 180 libras? Escrita en notación, la pregunta sería:
P(Y=180).
Mirando el gráfico, podrías pensar que la probabilidad de que una persona pese 180 libras es de alrededor del 50 %, pero eso no tiene sentido, ¿verdad? esa mitad de todas las personas pesan exactamente 180 libras! Lo que tienes que pensar es que alguien podría pesar 180 libras o podría pesar 180 libras y una fracción de onza de cualquier manera. podrían pesar 180.00001 libras o podrían pesar 179.999999999 libras. De hecho, las probabilidades de que alguien pese exactamente 180 libras son tan pequeñas que prácticamente son cero.

Otra forma de ver esto es que si dibujara el «área» para una pregunta como esta, en realidad sería solo una línea. ¡Y una recta tiene área cero!

Nota : Usamos una distribución normal en el ejemplo anterior, pero las funciones de distribución de probabilidad pueden tener cualquier forma, incluidas distribuciones uniformes y distribuciones exponenciales .

TI 83 Función NormalPDF

La función TI 83 normalPDF , accesible desde el menú DISTR, calculará la función de distribución de probabilidad normal, dada la media μ y la desviación estándar σ. La función en realidad no te da una probabilidad, porque la curva de distribución normal es continua. Sin embargo, puede usarlo para trazar una curva de campana y encontrar valores de x y valores de y para puntos en la curva.

Para otros comandos de distribución normal en la TI 83 (como la normalCDF de la TI 83 ), visite el menú de estadísticas de la TI 83 .

Función TI 83 NormalPDF: Pasos

Problema de muestra : Grafique una curva de campana en la calculadora TI 83 con una media de 100 y una desviación estándar de 15. Use la función NormalPDF.

Paso 1: Presione Y=.

Paso 2: presione 2do VARS 1 para obtener «PDF normal».

Paso 3: presione el botón X, T, θ, n , luego la media (100), luego la desviación estándar, 15. Cierre los paréntesis.

Paso 4: Presione VENTANA.

Paso 5: Cambie los valores de la ventana a lo siguiente (escriba los valores en los cuadros correspondientes):
Xmin=100-3*15
Xmax=100+3*15
Xscl=1
Ymin=0
Ymax=normalpdf(100,100,15)
Notas:

1. El x-min/x-max se establece en la media, menos/más tres desviaciones estándar, ya que esta es una curva de campana, por lo que +/- 3 desviaciones estándar mostrarán la curva completa.
2. Ymax usa la función normalpdf para determinar el valor máximo de y en la media (el pico de la curva)

Paso 6: Presione GRÁFICO . La TI 83 graficará una curva de distribución normal en su pantalla.

Paso 7: Presione TRACE y luego escriba cualquier número para encontrar el valor de y. Para este ejemplo, escriba 80 y luego presione ENTER.

¡Así es como se usa la TI 83 NormalPDF!

Sugerencia: una media de cero y una desviación estándar de son los valores predeterminados para una distribución normal en la calculadora, si no establece esos valores.

¿Perdiste tu guía? Descargue uno nuevo aquí desde el sitio web de TI.

¡ Visite nuestro canal de Youtube para obtener más ayuda y consejos sobre estadísticas!