Actualizado por ultima vez el 1 de octubre de 2021, por Luis Benites.
Conclusiones clave :
- La paradoja de Bertrand, que se refiere a las probabilidades, en realidad no es una paradoja en absoluto.
- El problema está en la redacción, no en las situaciones reales.
- Se puede ilustrar un ejemplo con el problema del “triángulo equilátero dibujado dentro de un círculo”.
¿Qué es la paradoja de Bertrand?
La paradoja de Bertrand muestra que si no se definen bien las probabilidades, el mecanismo que genera las variables aleatorias tampoco estará bien definido [1]. Esto conduce a una paradoja: una situación confusa y contradictoria.
La paradoja de Bertrand fue una de las razones por las que la probabilidad clásica cayó en desgracia a principios del siglo XX. Sin embargo, en realidad no es una paradoja en absoluto; si tiene cuidado de definir sus espacios de probabilidad, entonces la paradoja no existe .
Orígenes de la paradoja de Bertrand
En su tratado de 1889 Calculs des Probabilidades , Bertrand preguntó:
“Si elegimos al azar dos puntos en la superficie de una esfera, ¿cuál es la probabilidad de que la distancia entre ellos sea menor que 10?”
Bertrand ofreció dos soluciones.
- La probabilidad de que cierto segmento de la superficie de la esfera contenga los dos puntos es proporcional al área del segmento como un todo.
- Un arco dado en un círculo máximo, con los dos puntos, es proporcional a la longitud del arco.
De hecho, hay varias maneras de abordar el problema. Esto conduce a múltiples soluciones y probabilidades.
Ejemplo de la paradoja de Bertrand
Para ilustrar la paradoja desde un ángulo ligeramente diferente (juego de palabras), echemos un vistazo a un triángulo equilátero dibujado dentro de un círculo.
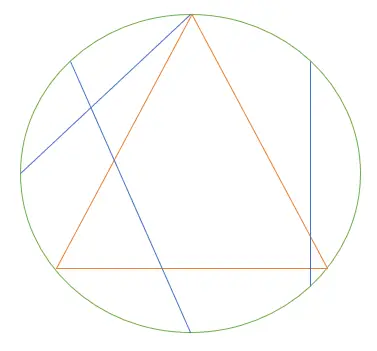
Un triángulo equilátero (naranja) inscrito en un círculo. Tres cuerdas se muestran en azul.
Lo que queremos saber es que, si elegimos una cuerda al azar (un segmento de línea dibujado entre dos puntos de la circunferencia), ¿cuáles son las probabilidades de que la cuerda sea más larga que un lado del triángulo?
La solución parece bastante simple. Elija un punto aleatorio en el círculo, utilícelo como punto medio para una cuerda: esta forma de elegir una cuerda aleatoria da una probabilidad de 0,25 [2]. Pero obviamente esta no es la única forma de encontrar un acorde. Podríamos elegir un punto en el perímetro para comenzar (que dará una probabilidad de 2/3) o elegir un radio al azar, luego un punto al azar (probabilidad = ½).
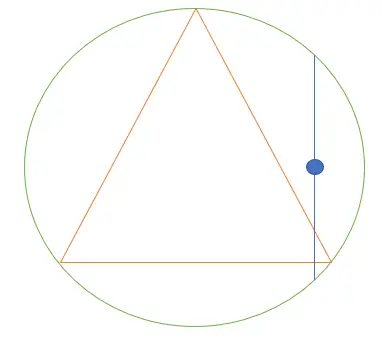
Todas las soluciones son válidas. Sin embargo, no todos pueden ser válidos al mismo tiempo , de ahí la paradoja. La razón de la paradoja es que el problema inicial está mal planteado. No nos dieron ninguna regla para elegir nuestros acordes, por lo que dejó la puerta abierta para múltiples interpretaciones.
Referencias
[1] Chang, M. Paradojas en la inferencia científica . CRC Press, 2012.[2] Bartlett, P. (2014). Clase 2: La paradoja de Bertrand. Recuperado el 2 de junio de 2020 de: http://web.math.ucsb.edu/~padraic/ucsb_2013_14/math7h_s2014/math7h_s2014_lecture2.pdf

