Actualizado por ultima vez el 21 de abril de 2022, por Luis Benites.
Las probabilidades logarítmicas juegan un papel central en la regresión logística . Cada probabilidad se puede convertir fácilmente en probabilidades logarítmicas , encontrando la razón de probabilidades y tomando el logaritmo .
A pesar de la conversión relativamente simple, las probabilidades logarítmicas pueden ser un poco esotéricas. Jaccard (2001, p. 10) las llama “… contrarias a la intuición y difíciles de interpretar”, especialmente si no se tiene una formación estadística sólida. Dicho esto, las fórmulas son relativamente simples, incluso si los resultados son un poco difíciles de descifrar.
Conversiones: Probabilidad a Cuotas a Registro de Cuotas
La probabilidad, las razones de probabilidades y las probabilidades logarítmicas son lo mismo, solo que se expresan de diferentes maneras. Es similar a la idea de la notación científica: el número 1000 se puede escribir como 1,0*10 3 o incluso 1*10*10*10. Lo que funciona para una persona, o una ecuación, podría no funcionar para otra. En muchos casos, simplemente puede elegir qué formato desea utilizar . Otras veces (por ejemplo, está publicando un artículo o está utilizando la regresión logística), es posible que se vea obligado a adoptar un formato particular.
La probabilidad es la probabilidad de que suceda un evento. Por ejemplo, podría haber un 80% de probabilidad de lluvia hoy.
Las probabilidades (más técnicamente, las probabilidades de éxito ) se definen como probabilidad de éxito/probabilidad de fracaso. Entonces, las probabilidades de éxito (80% de probabilidad de lluvia) tienen una probabilidad de fracaso (20% de probabilidad de que no llueva); como una ecuación (la “ razón de probabilidades ”), eso es .8/.2 = 4. Logaritmo de
probabilidades es el logaritmo de las probabilidades. Ln(4) = 1,38629436 ≅ 1,386.
La conversión a probabilidades logarítmicas da como resultado una simetría alrededor de cero, que es más fácil de analizar, como se muestra en la siguiente tabla (Jaccard, 2001):
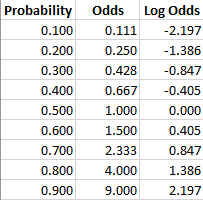
Log Odds y la función Logit
La razón de posibilidades es la probabilidad de éxito/probabilidad de fracaso. Como ecuación, eso es P(A)/P(-A), donde P(A) es la probabilidad de A, y P(-A) la probabilidad de ‘no A’ (es decir, el complemento de A).
Tomando el logaritmo de la razón de probabilidades, obtenemos las probabilidades logarítmicas de A, que se pueden escribir como
registro(A) = registro(P(A)/P(-A)),
Dado que la probabilidad de que suceda un evento, P(-A) es igual a la probabilidad de que no suceda un evento, 1 – P(A), podemos escribir las probabilidades logarítmicas como
Donde:
- p = la probabilidad de que suceda un evento
- 1 – p = la probabilidad de que un evento no suceda
Cuando la variable de una función representa una probabilidad, p (como en la función anterior), se llama función logit .
Uso de probabilidades de registro
A veces elegimos usar probabilidades logarítmicas en lugar de medidas de probabilidad más básicas porque se actualizan muy fácilmente con nuevos datos.
Por ejemplo, suponga que tiene un 5% de posibilidades de que un ladrón entre a su puerta en una noche determinada. Tienes un perro guardián, pero no es muy confiable; ladrará la mitad de las veces si viene un ladrón, y solo la cuarta parte de las veces si la persona que pasa por ahí es un hombre honesto. Ahora imagina que escuchas pasos y el perro ladra.
Antes de que su perro ladrara, las probabilidades logarítmicas de un ladrón eran ln(.05/.95) = ln(1/19), o -2.9444. A eso lo llamamos sus probabilidades de registro anteriores para el ladrón. La razón de probabilidad de un ladrido es simplemente la probabilidad de un ladrido con un ladrón (1/2) sobre la probabilidad de un ladrido sin ladrón (1/4), y para encontrar las probabilidades logarítmicas tomamos el logaritmo de eso: ln ((1/2)/(1/4)) = log(2) = 0,6931. Ahora, las probabilidades logarítmicas posteriores del ladrón (las probabilidades logarítmicas de que haya un ladrón, dado que acabas de escuchar ladrar al perro) son -2,9444 + 0,6931, o -2,2513.
Dado que ln (odds ratio) = log odds, e log odds = odds ratio. Entonces, para convertir nuestro -2.2513 anterior en una razón de probabilidades, calculamos e -2.2513 , que resulta ser aproximadamente 0.1053:1. Entonces la probabilidad de que tengamos un ladrón es 0.1053/1.1053 = 0.095, entonces 9.5 %. Observe cómo convertimos la razón de probabilidades en una probabilidad al dividir la primera parte de la razón por la suma de ambas partes (el total). Note también que llegamos a nuestra respuesta final sin ningún cálculo involucrado, asumiendo, por supuesto, que tenemos una calculadora para ayudarnos con los logaritmos.
Hemos usado logaritmos naturales aquí ( base e ); en realidad puede usar registros en cualquier base, solo necesita ser consistente.
Referencias
Eckel, S. (2008). Interpretación de modelos de regresión logística. http://www-hsc.usc.edu/~eckel/biostat2/notes/notes14.pdf
Jaccard, J. (2001) Efectos de interacción en la regresión logística , número 135. SAGE.
Rotella, J. (nd) Probabilidad, Log Odds y Odds. Recuperado el 14 de diciembre de 2017 de: http://www.montana.edu/rotella/documents/502/Prob_odds_log-odds.pdf

