Contenido de este artículo
Actualizado el 12 de abril de 2022, por Luis Benites.
¿Qué es la asimetría de Bowley?
 El sesgo de Bowley es una forma de averiguar si tiene una distribución sesgada positiva o negativamente. Una de las formas más populares de encontrar la asimetría es la fórmula Pearson Mode Skewness . Sin embargo, para usarlo, debe conocer la media, la moda (o mediana) y la desviación estándar de sus datos. A veces es posible que no tenga esa información; En su lugar, es posible que tenga información sobre sus cuartiles . Si ese es el caso, puede usar Bowley Skewness como alternativa para obtener más información sobre la asimetría de su distribución. Es muy útil si tiene valores de datos extremos ( outliers ) o si tiene una distribución abierta .
El sesgo de Bowley es una forma de averiguar si tiene una distribución sesgada positiva o negativamente. Una de las formas más populares de encontrar la asimetría es la fórmula Pearson Mode Skewness . Sin embargo, para usarlo, debe conocer la media, la moda (o mediana) y la desviación estándar de sus datos. A veces es posible que no tenga esa información; En su lugar, es posible que tenga información sobre sus cuartiles . Si ese es el caso, puede usar Bowley Skewness como alternativa para obtener más información sobre la asimetría de su distribución. Es muy útil si tiene valores de datos extremos ( outliers ) o si tiene una distribución abierta .
Fórmula de la asimetría de Bowley.
Mire el video para obtener una descripción general:
Ejemplo resuelto de la asimetría de Bowley Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí.
Sesgo de Bowley = (Q 3 +Q 1 – 2Q 2 ) / (Q 3 – Q1)
- La asimetría = 0 significa que la curva es simétrica .
- La asimetría > 0 significa que la curva tiene una asimetría positiva.
- La asimetría < 0 significa que la curva tiene una asimetría negativa.
Ejemplo resuelto de la asimetría de Bowley
P. Encuentre la asimetría de Bowley para el siguiente conjunto de datos:
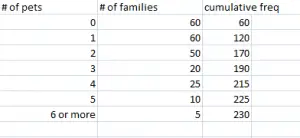
Paso 1: encuentre los cuartiles para el conjunto de datos. Querrá buscar la «n-ésima» observación utilizando las siguientes fórmulas: Q
1 = (frecuencia acumulada total + 1 / 4) observación = (230 + 1 / 4) = 57,75 Q 2 = (frecuencia acumulada total + 1 / 2) ésima observación = (230 + 1 / 2 ) = 115,5 Q 3 = 3 (total cum freq + 1 / 4) ésima observación = 3(230 + 1 / 4) = 173,25
Paso 2: Mire en su tabla para encontrar las enésimas observaciones que calculó en el Paso 1:
Q 1 = 57,75 a observación = 0 Q 2 = 115,5 a observación = 1 Q 3 = 173,25 a observación = 3
Paso 3: Introduzca los valores anteriores en la fórmula:
S kq = (Q 3 + Q 1 – 2Q 2 ) / (Q 3 – Q 1 )
S kq = (3 + 0 – 2) / (3 – 0) = 1 /3
S kq = + 1/3, por lo que la distribución tiene un sesgo positivo.
Por qué Bowley Skewness funciona.
En una distribución simétrica , como la distribución normal , el primer (Q 1 ) y el tercer (Q 3 ) cuartiles están a la misma distancia de la media (Q 2 ). En otras palabras, (Q 3 -Q 2 ) y (Q 2 -Q 1 ) serán iguales. Si tiene una distribución sesgada , habrá una diferencia entre esos dos valores.
Limitaciones de la asimetría de Bowley.
Bowley Skewness es una medida absoluta de asimetría. En otras palabras, le dará un resultado en las unidades en las que se encuentra su distribución. Eso se compara con la asimetría del modo de Pearson, que le da resultados en una unidad adimensional: la desviación estándar . Esto significa que no puede comparar la asimetría de diferentes distribuciones con diferentes unidades usando Bowley Skewness.
Fórmula alternativa de Bowley Skewness.
Según Business Statistics , Bowley reconoció que la fórmula Bowley Skewness no podía usarse para comparar diferentes distribuciones con diferentes unidades. Por ejemplo, no se puede comparar una distribución medida en alturas en cm con una de pesos en libras. Ofreció una fórmula alternativa. Debe usar esta fórmula si desea comparar diferentes distribuciones con diferentes unidades:
Asimetría relativa = ((Q 3 + Q 1 ) – (2 * Mediana ))/ (Q 3 – Q 1 ).
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
