Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 12 de enero de 2022, por Luis Benites.
Correlación biserial de puntos
1. ¿Qué es la correlación biserial de puntos?
El coeficiente de correlación biserial puntual, r pbi , es un caso especial del coeficiente de correlación de Pearson . Mide la relación entre dos variables:
- Una variable continua (debe ser una escala de razón o una escala de intervalo ).
- Una variable naturalmente binaria .*
Muchas situaciones diferentes requieren analizar un vínculo entre una variable binaria y una variable continua. Por ejemplo:
- ¿El Medicamento A o el Medicamento B mejoran la depresión?
- ¿Es probable que las mujeres o los hombres ganen más como enfermeras?
Fórmula
La fórmula para el coeficiente de correlación biserial puntual es:
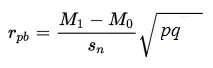
- M 1 = media (para toda la prueba) del grupo que recibió la variable binaria positiva (es decir, el “1”).
- M 0 = media (para toda la prueba) del grupo que recibió la variable binaria negativa (es decir, el “0”).
- S n = desviación estándar para toda la prueba.
- p = Proporción de casos en el grupo “0”.
- q = Proporción de casos en el grupo “1”.
La mayoría de las personas no trabajarán esta fórmula a mano, ya que la mayoría de los paquetes de software estadístico pueden calcular el coeficiente por usted.
Interpretación
Al igual que otros coeficientes de correlación , el punto biserial va de 0 a 1, donde 0 es sin relación y 1 es una relación perfecta.
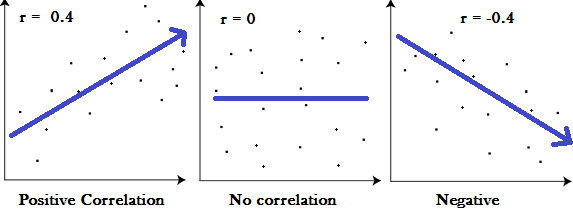
Gráficos que muestran una correlación de -1, 0 y +1
Precauciones :
- *Si fuerza intencionalmente los datos para que se conviertan en binarios para que pueda ejecutar la correlación biserial de puntos, tal vez al dividir las variables de relación continua en dos segmentos, hará que sus resultados sean menos confiables. Hay excepciones a esta regla general. Por ejemplo, podría separar los puntajes de las pruebas o los GPA en aprobado/reprobado, creando una variable binaria lógica. Un ejemplo forzando de manera antinatural una escala en una variable binaria: decir que las personas de menos de 5’9 ″ son «Bajas» y las de más de 5’9 «son «altas».
- Una suposición para esta prueba es que las variables son aleatoriamente independientes. Por lo tanto, el punto biserial no debe utilizarse para analizar resultados experimentales; use Regresión lineal con variables ficticias en su lugar.
2. Correlación Biserial
La correlación biserial es casi lo mismo que la correlación biserial puntual, pero una de las variables son datos ordinales dicotómicos y tienen una continuidad subyacente. Por ejemplo, el nivel de depresión puede medirse en una escala continua, pero puede clasificarse dicotómicamente como alto/bajo.
La fórmula es:
r b = [(Y 1 – Y 0 ) * (pq/Y) ] /σ y ,
Donde:
- Y 0 = puntuación media para pares de datos para x=0,
- Y 1 = puntuación media para pares de datos para x=1,
- q = proporción de pares de datos para x=0,
- p = proporción de pares de datos para x=1,
- σ y = desviación estándar de la población.
Y es la altura de la distribución normal estándar en z, donde P(z'<z) = q y P(z’>z) = p.
Si conoce la correlación punto-biserial, también puede encontrar la correlación biserial con la siguiente fórmula (Sheskin, 2011): Donde: Pr[Z ≥u|Z~N(0,1)] = p 1 .
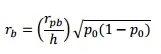
![]()
Referencias:
Sheskin, D. (2011). Manual de procedimientos estadísticos paramétricos y no paramétricos (5ª ed.). Boca Ratón, FL: CRC Press.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
