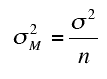Actualizado por ultima vez el 27 de noviembre de 2021, por Luis Benites.
¿Qué es el cuadrado medio entre?
La media cuadrática entre le da una idea de las diferencias entre las medias de las muestras . Su mayor uso es encontrar la relación F en una prueba ANOVA . Dependiendo del autor, se denota por MS(B), σ 2 o 
. Por sí solo, MS(B) no es una estadística muy útil. A diferencia de la media o la desviación estándar , no puede usarla para realizar comparaciones directas. Sin embargo, si el error cuadrático medio (MSE) y MS(B) son aproximadamente iguales, esta es una buena indicación de que las medias de su población son iguales. Si las medias de la población son iguales, entonces MS(B) se puede usar para estimar la varianza , σ 2 . Si las medias de la población no son iguales, MS(B) sobreestimará σ 2 .
Uso
El cuadrado medio entre se utiliza para calcular la relación F (a veces denominada valor F):
Relación F = MSB/MSE.
Para muestras pequeñas, la relación F puede no ser útil. Pero para muestras más grandes, MSB y MSE suelen ser iguales y, por lo tanto, devolverían una relación F de 1. Las relaciones F grandes (más de 2 o más) indican que las medias de la población no son iguales.
MS(B) también se utiliza para calcular la suma total de los cuadrados , que es igual a la suma de los cuadrados medios dentro y entre los cuadrados medios.
Suma de cuadrados SS = Dentro del cuadrado medio MS(W) + Cuadrado medio entre MS(B)
En general, las medias muestrales más pequeñas dan como resultado valores más pequeños para MS(B).
Fórmula
MS(B) se calcula a partir de las medias muestrales (en comparación con MSE, que se calcula a partir de las varianzas muestrales). Para encontrar MS(B), divida la variación entre grupos (SS entre ) dividida por los grados de libertad entre grupos (k-1). Como fórmula, eso es:
MS(B) = SS entre / (k-1)
Como alternativa, puede multiplicar n (el tamaño de la muestra) por la varianza de la distribución muestral de la media: por ejemplo, si la varianza de las medias muestrales es 0,199 y el tamaño de su muestra es 39, entonces MS(B) = 0,199*39 = 38,61.
