Actualizado por ultima vez el 26 de noviembre de 2021, por Luis Benites.
¿Qué es la prueba Goldfeld Quandt?
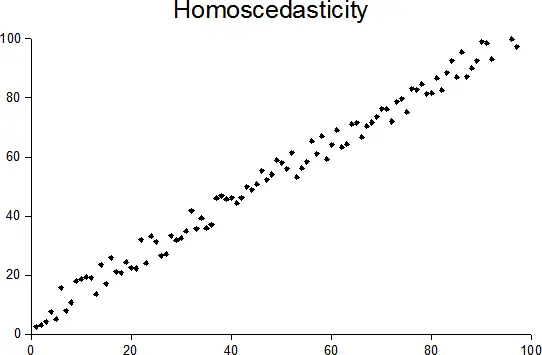
Los datos homocedásticos están dispersos uniformemente alrededor de la línea. Imagen: Sreebot| Wikimedia Commons
La prueba Goldfeld Quandt es una prueba utilizada en el análisis de regresión para probar la homocedasticidad . Compara las varianzas de dos subgrupos; un conjunto de valores altos y un conjunto de valores bajos. Si las varianzas difieren, la prueba rechaza la hipótesis nula de que las varianzas de los errores no son constantes.
Aunque Goldfeld y Quandt describieron dos tipos de prueba en su artículo ( paramétrica y no paramétrica ), el término «prueba de Quandt Goldfeld» generalmente significa prueba paramétrica. La suposición para la prueba es que los datos se distribuyen normalmente .
La estadística de prueba para esta prueba es la razón de los errores residuales cuadráticos medios para las regresiones en los dos subconjuntos de datos. Esto corresponde a la prueba F para la igualdad de varianzas. Se pueden utilizar tanto las pruebas de una cola como las de dos colas .
Pasos para ejecutar la prueba
- Ordena los datos en orden ascendente. Este paso depende de que usted, el investigador, encuentre una forma adecuada de ordenar la muestra. Por lo general, ordenar por magnitud de x (una variable independiente) funciona.
- Divide tus datos en tres partes*.
- Deja las observaciones en la parte media.
- Ejecute un análisis de regresión separado en las partes superior e inferior (en otras palabras, los grupos con valores altos de x y valores bajos de x). Después de cada regresión, encuentre la Suma residual de cuadrados .
- Calcular la relación de la suma de cuadrados Residual, donde RSS 2 es el conjunto de valores altos y RSS 1 es el conjunto de valores bajos: (RSS 2 /df)/(RSS 1 /df).
- Aplique la regla de decisión convencional para una prueba F. En general, los valores grandes de F suelen indicar que las varianzas son diferentes.
*Goldfeld y Quandt no especificaron cuántas observaciones centrales eliminar. Usar un tercio es opcional, pero recomendado. Si aumenta el tamaño de esta parte central, aumentará la potencia de la prueba. Sin embargo, los grados de libertad del estadístico de prueba se reducirán. También se recomienda que, a medida que aumenta el tamaño de la muestra, disminuya el tamaño de esta parte central.
Referencia :
SM Goldfeld y RE Quandt (1965), Algunas pruebas de homocedasticidad. Revista de la Asociación Estadounidense de Estadística 60, 539–547

