Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 26 de noviembre de 2021, por Luis Benites.
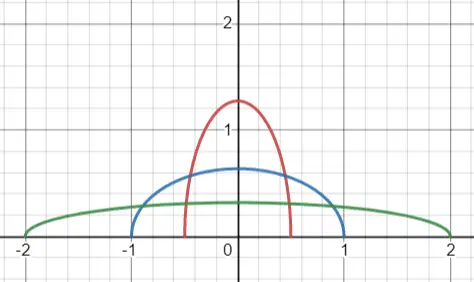
Distribución semicircular de Wigner con R = 0,5 (rojo), 1 (azul) y 2 (verde).
La distribución de semicírculo (también llamada distribución de semicírculo de Wigner ) es una distribución de probabilidad continua con forma de semicírculo a escala. Está centrado en el origen (0, 0) con radio R > 0 en el intervalo [-R, R].
La función de densidad de probabilidad de la distribución semicircular es:
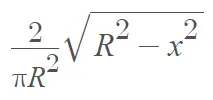
Una variante es la distribución semicircular de potencia PS(θ, R), que tiene PDF:
f θ (x, R) = c′ θ, R (f 0 (x; R)) 2θ + 1) = c θ, R (R 2 – x 2 ) θ + ½ 1 |x| ≤ , R
Donde R es el parámetro de rango y θ es el parámetro de forma .
Usos de la distribución semicircular
La distribución en semicírculo juega un papel importante en muchas áreas de las matemáticas, incluidas las matemáticas aplicadas. Por ejemplo, el físico EP, Wigner demostró que es la medida espectral asintótica de los conjuntos de Wigner de matrices aleatorias; la ley del semicírculo local establece que la distribución de valores propios de una matriz de Wigner está cerca de la distribución del semicírculo de Wigner [1]. La ley del semicírculo también aparece en física, en un movimiento browniano cuántico en el espacio de Fock del bosón libre [2]. La distribución es también la distribución límite de una cadena de Markov de diagramas de Young [3] y es la distribución límite en la versión libre del teorema central del límite [4].
Referencias
Gráfico de la distribución del semicírculo de Wigner creado con Desmos .
[1] Benaych-Georges, F. & Knowles, A. Conferencias sobre la ley del semicírculo local para matrices de Wigner .
[2] Hashimoto, Y. DEFORMACIONES DE LA LEY DEL SEMICIRCULO DERIVADAS DE PASEOS ALEATORIOS EN GRUPOS LIBRES.
[3] Arizmendi, O. & Pérez-Abreu, V. (2010). SOBRE LA DIVISIBILIDAD INFINITA NO CLÁSICA DE LAS DISTRIBUCIONES EN SEMICÍRCULOS DE POTENCIA. Comunicaciones sobre Análisis Estocástico. vol. 4, núm. 2. 161-178. Recuperado el 30 de diciembre de 2021 de: http://personal.cimat.mx:8181/~pabreu/4-2-02%5B221%5D.pdf
[4] Barndorff-Nielsen, O. & Thorbjørnsen, S. Levy leyes en probabilidad libre .
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
