Distribución de matrices

Actualizado por ultima vez el 2 de abril de 2022, por Luis Benites.

La distribución de matriz se refiere a la distribución condicional de variables aleatorias independientes X1 (dado X2, …, Xn). Como tal, a menudo se usa como sinónimo de una distribución condicional (por ejemplo, Kotz et al. [1], Giri & Banerjee [2], Wadworth & Bryan [3]).

La Enciclopedia de Ciencias Estadísticas [4] da un ejemplo de una distribución de matriz de X

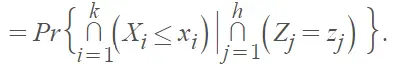
La varianza de esta distribución se denomina varianza de matriz; si la varianza no depende de X2, … ,Xn , la varianza es homocedástica [5]. Su matriz de varianza-covarianza se llama matriz de matriz-varianza-covarianza.

Distribución de matrices en estadística teórica y aplicada

Como se señaló anteriormente, la distribución de matriz se usa comúnmente como sinónimo de distribución condicional. Significan lo mismo, pero es más probable que vea el término distribución de matriz en estadística aplicada y distribución condicional en estadística teórica [6]. La distribución de la matriz se denota por

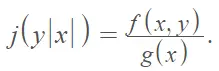
Puedes pensar en esto como la densidad de y para un valor fijo de x.

Referencias
[1] Kotz, S. et al. (2000). Distribuciones Multivariadas Continuas, Volumen 1 Modelos y Aplicaciones. John Wiley & Sons.

[2] Giri, P. y Banerjee, J. (2021). Herramientas y Técnicas Estadísticas. Editores Académicos.

[3] Wadsworth, G. y Bryan, J. (1960). Introducción a la Probabilidad ya las Variables Aleatorias. McGraw-Hill.

[4] Vidakovic, B. et al. (Editorial) (2005). Enciclopedia de Ciencias Estadísticas, Volumen 3. Wiley.

[5] Johnson, Kotz y Balakrishnan, (1994), Distribuciones univariadas continuas , Volúmenes I y II, 2.º. Ed., John Wiley and Sons.

[6] Haight (ed.) (1963). Teorías Matemáticas del Flujo de Tráfico. Ciencia de Elsevier