Actualizado por ultima vez el 2 de abril de 2022, por Luis Benites.
La distribución hiperexponencial (también llamada distribución exponencial mixta o exponencial de fase m paralela ) es creada por una mezcla probabilística de distribuciones exponenciales . Es una generalización de la distribución de Erlang y un caso especial de la distribución de tipo fase (hecha por una convolución o mezcla de distribuciones exponenciales) [1].
Se llama hiperexponencial porque la distribución siempre tiene un coeficiente de variación mayor que 1 [2].
Parámetros y forma de distribución hiperexponencial
La distribución hiperexponencial se define sobre el intervalo semiabierto [0, ∞). La forma de la distribución está determinada por dos vectores α (probabilidades de fase con valores de 0 a 1) y λ (tasas de fase, que son valores reales ).
El PDF es: Donde:
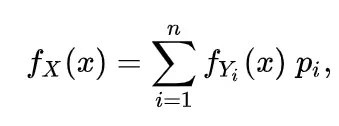
- Y i = una variable aleatoria distribuida exponencialmente con parámetro de tasa i.
- p i = probabilidad de que X tenga una distribución exponencial con tasa λ.
En términos generales, la distribución hiperexponencial disminuye monótonamente con colas ligeras . Esto significa que la PDF disminuye exponencialmente para valores de x grandes.
Etapas de una distribución hiperexponencial
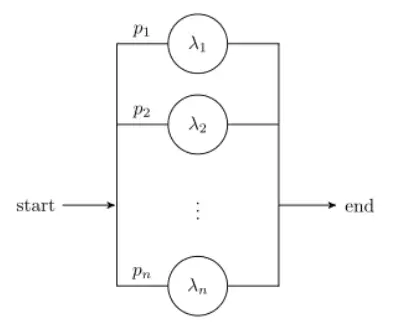
Sistema de colas equivalente a una distribución hiperexponencial. Imagen: Gareth Jones | Wikimedia Commons.
La distribución hiperexponencial surge cuando un proceso tiene fases alternas, lo que significa que solo una de las muchas fases paralelas posibles ocurrirá en cualquier experimento en particular. Si las fases alternas tienen distribuciones exponenciales independientes, entonces la distribución es hiperexponencial [3].
Las distribuciones hiperexponenciales pueden tener cualquier número de etapas. Para cada etapa, se deben especificar parámetros que definan la probabilidad de recibir el servicio y la tasa de servicio en cada etapa.
Por ejemplo, un hiperexponencial de dos etapas, creado a partir de dos exponenciales, tiene tres parámetros: p, λ 1 y λ 2 [4]:
- p: la probabilidad de recibir el servicio a la tasa λ 1 .
- p – 1: la probabilidad de recibir el servicio a la tasa λ 2 .
Referencias
Imagen del sistema de colas: Gareth Jones, CC BY-SA 3.0
[1] Paquete ‘sdprisk’ .
[2] (2013) Distribución hiperexponencial. En: Gass SI, Fu MC (eds) Encyclopedia of Operations Research and Management Science. Springer, Boston, MA.
[3] Iyer, R. (1999). Distribuciones importantes. Recuperado el 2 de abril de 2021 de: /distribución-erlang/
[4] CS 547 Clase 14: Otras distribuciones de tiempo de servicio

