Actualizado por ultima vez el 3 de abril de 2022, por Luis Benites.
¿Qué es una distribución trapezoidal?
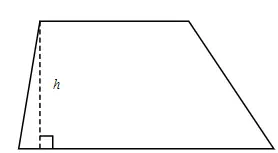
Un trapezoide.
Las distribuciones trapezoidales tienen la forma de un trapezoide: un cuadrilátero con dos lados paralelos y dos no paralelos. Tienden a ser una buena opción para los datos que muestran un crecimiento bastante rápido, un período de nivelación y luego una caída bastante rápida. Las tres etapas son funciones lineales : la primera etapa es creciente con pendiente positiva ; El período de nivelación es constante y la etapa final es decreciente con pendiente negativa.
Van Dorp & Kotz definen los parámetros de la distribución como:
- a = valor mínimo de la variable aleatoria ,
- b = modo inferior (donde comienza la etapa constante),
- c = modo superior (donde termina la etapa constante),
- d = valor máximo de la variable aleatoria ,
- m = tasa de crecimiento para el período entre a y b,
- n = tasa de decaimiento para el período entre c y d,
- α = relación límite , fx(b)/fx(c) que Kotz y Van Dorp definen como “la probabilidad relativa de las capacidades en la etapa [a,b] y el comienzo de la etapa de descomposición [c, d]”.
Tenga en cuenta que la moda de esta distribución no es única; puede tomar cualquier valor entre el modo inferior c y el modo superior d.
PDF de la Distribución Trapezoidal
La Función de Densidad de Probabilidad (PDF) para la distribución trapezoidal (De Dorp & Kotz, 2003) es: Donde:
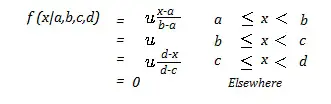
- μ = 2/(d + c – b – a) -1
- un ≤ segundo ≤ c ≤ re
FCD
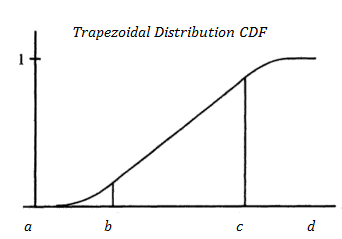La función de distribución acumulativa trapezoidal es 0 para x < a y 1 para x ≥ d. De lo contrario, es lineal entre b y c, y cuadrática para a → b y c → d:
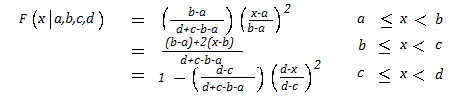
Distribuciones Similares
- La distribución uniforme es un caso especial de la distribución trapezoidal; No tiene una etapa de crecimiento o decaimiento, por lo que a (el mínimo) = c (el modo inferior) y d (el máximo) = b (el modo superior).
- La distribución triangular es también un caso especial de la trapezoidal; Le falta la etapa constante, por lo que b (el modo inferior) = c (el modo superior).
Referencias:
Kotz, S. & Dorp. R. (2004). Más allá de Beta: otras familias continuas de distribuciones con soporte y aplicaciones limitadas . Científico Mundial.
Van Dorp, Jet. Alabama,. (2004). Un procedimiento de obtención de la distribución trapezoidal generalizada con una etapa central uniforme. Decision Analysis, 4(3):156–166, septiembre de 2007.
Van Dorp, J. & Kotz, S.(2003) Distribuciones trapezoidales generalizadas. Métrika, vol. 58, número 1, julio.
