Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 7 de enero de 2022, por Luis Benites.
1. ¿Qué es una función generadora de momentos?
Las funciones generadoras de momentos (MGF) son una forma de encontrar momentos como la media (μ) y la varianza (σ 2 ). Son una forma alternativa de representar una distribución de probabilidad con una función simple de una variable .
Cada distribución de probabilidad tiene un MGF único , lo que significa que son especialmente útiles para resolver problemas como encontrar la distribución de sumas de variables aleatorias . También se pueden usar como prueba del Teorema del Límite Central .
No existe una definición intuitiva de qué es exactamente un MGF ; es solo una herramienta computacional . Piensa en ello como una fórmula, de la misma manera que y = mx + b te permite crear funciones lineales , la fórmula MGF te ayuda a encontrar momentos.
Cómo encontrar un MGF
Encontrar un MGF para una variable aleatoria discreta implica la suma ; para variables aleatorias continuas, se utiliza el cálculo. En realidad, es muy simple crear funciones generadoras de momentos si se siente cómodo con la suma y/o la diferenciación y la integración : Para las fórmulas anteriores, f(x) es la función de densidad de probabilidad de X y el rango de integración (listado como -∞ a ∞) cambiará dependiendo del rango para el que esté definida su función.
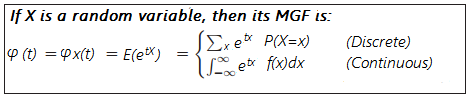
Ejemplo : Encuentre el MGF para e- x .
Solución :
Paso 1: Sustituya e -x para fx(x) para obtener: Tenga en cuenta que cambié el límite integral inferior a cero, porque esta función solo es válida para valores superiores a cero.
Paso 2: Integrar. El MGF es 1/(1-t).
La función generadora de momentos solo funciona cuando la integral converge en un número particular. La integral anterior diverge (se esparce) para valores de t de 1 o más, por lo que el MGF solo existe para valores de t menores que 1. Descubrirá que la mayoría de las distribuciones continuas no están definidas para valores más grandes (digamos, por encima de 1) . Por lo general, esto no es un problema: para encontrar los valores esperados y las varianzas , solo se necesita encontrar el MGF para valores pequeños de t cercanos a cero.
Usando el MGF
Una vez que haya encontrado la función generadora de momentos, puede usarla para encontrar el valor esperado, la varianza y otros momentos.
- M(0) = 1,
- M′(0) = E(X),
- M′′( 0 ) = E(X2 ),
- M′′′(0) = E(X 3 )
y así;
Var(X) = M′′(0) − M′(0) 2 .
Ejemplo: encuentre E(X 3 ) usando el MGF (1-2t) -10 .
Paso 1: encuentre la tercera derivada de la función (la lista anterior define M′′′(0) como igual a E(X 3 ); antes de que pueda evaluar la derivada en 0, primero debe encontrarla):
M ′′′(t) = (−2) 3 (−10)(−11)(−12)(1 − 2 t ) -13
Paso 2: Evaluar la derivada en 0:
M′′′(0) = (−2) 3 (−10)(−11)(−12)(1 − 2 t ) -13
= (−2) 3 (− 10)(−11)(−12)(1)
= 10,560.
Solución : E(X 3 ) = 10,560.
¿Qué es una función generadora de probabilidad?
Una función generadora de probabilidad contiene la misma información que una función generadora de momentos, con una diferencia importante: la función generadora de probabilidad se usa normalmente para variables aleatorias con valores enteros no negativos .
Referencias
Papoulis, A. Probabilidad, variables aleatorias y procesos estocásticos , 2ª ed. Nueva York: McGraw-Hill, págs. 145-149, 1984.
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
