Actualizado por ultima vez el 22 de noviembre de 2021, por Luis Benites.
1. ¿Qué es una función generadora de momentos?
Las funciones generadoras de momentos (MGF) son una forma de encontrar momentos como la media (μ) y la varianza (σ 2 ). Son una forma alternativa de representar una distribución de probabilidad con una función simple de una variable .
Cada distribución de probabilidad tiene un MGF único , lo que significa que son especialmente útiles para resolver problemas como encontrar la distribución de sumas de variables aleatorias . También se pueden usar como prueba del Teorema del Límite Central .
No existe una definición intuitiva de qué es exactamente un MGF ; es solo una herramienta computacional . Piensa en ello como una fórmula, de la misma manera que y = mx + b te permite crear funciones lineales , la fórmula MGF te ayuda a encontrar momentos.
Cómo encontrar un MGF
Encontrar un MGF para una variable aleatoria discreta implica la suma ; para variables aleatorias continuas, se utiliza el cálculo. En realidad, es muy simple crear funciones generadoras de momentos si se siente cómodo con la suma y/o la diferenciación y la integración : Para las fórmulas anteriores, f(x) es la función de densidad de probabilidad de X y el rango de integración (listado como -∞ a ∞) cambiará dependiendo del rango para el que esté definida su función.
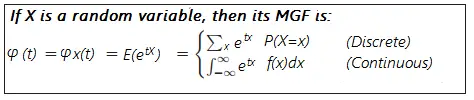
Ejemplo : Encuentre el MGF para e- x .
Solución :
Paso 1: Sustituya e -x para fx(x) para obtener: Tenga en cuenta que cambié el límite integral inferior a cero, porque esta función solo es válida para valores superiores a cero.
Paso 2: Integrar. El MGF es 1/(1-t).
La función generadora de momentos solo funciona cuando la integral converge en un número particular. La integral anterior diverge (se esparce) para valores de t de 1 o más, por lo que el MGF solo existe para valores de t menores que 1. Descubrirá que la mayoría de las distribuciones continuas no están definidas para valores más grandes (digamos, por encima de 1) . Por lo general, esto no es un problema: para encontrar los valores esperados y las varianzas , solo se necesita encontrar el MGF para valores pequeños de t cercanos a cero.
Usando el MGF
Una vez que haya encontrado la función generadora de momentos, puede usarla para encontrar el valor esperado, la varianza y otros momentos.
- M(0) = 1,
- M′(0) = E(X),
- M′′( 0 ) = E(X2 ),
- M′′′(0) = E(X 3 )
y así;
Var(X) = M′′(0) − M′(0) 2 .
Ejemplo: encuentre E(X 3 ) usando el MGF (1-2t) -10 .
Paso 1: encuentre la tercera derivada de la función (la lista anterior define M′′′(0) como igual a E(X 3 ); antes de que pueda evaluar la derivada en 0, primero debe encontrarla):
M ′′′(t) = (−2) 3 (−10)(−11)(−12)(1 − 2 t ) -13
Paso 2: Evaluar la derivada en 0:
M′′′(0) = (−2) 3 (−10)(−11)(−12)(1 − 2 t ) -13
= (−2) 3 (− 10)(−11)(−12)(1)
= 10,560.
Solución : E(X 3 ) = 10,560.
¿Qué es una función generadora de probabilidad?
Una función generadora de probabilidad contiene la misma información que una función generadora de momentos, con una diferencia importante: la función generadora de probabilidad se usa normalmente para variables aleatorias con valores enteros no negativos .
Referencias
Papoulis, A. Probabilidad, variables aleatorias y procesos estocásticos , 2ª ed. Nueva York: McGraw-Hill, págs. 145-149, 1984.
