Actualizado por ultima vez el 22 de noviembre de 2021, por Luis Benites.
El modelo oculto de Markov (HMM) es una forma relativamente sencilla de modelar datos secuenciales. Un modelo de Markov oculto implica que el modelo de Markov subyacente a los datos está oculto o es desconocido para usted. Más específicamente, solo conoce datos de observación y no información sobre los estados. En otras palabras, hay un tipo específico de modelo que produce los datos (un modelo de Markov) pero no sabes qué procesos los están produciendo. Básicamente, utiliza su conocimiento de los modelos de Markov para hacer una suposición informada sobre la estructura del modelo.
¿Qué es un modelo de Markov?
Para descubrir el modelo oculto de Markov, primero debe comprender qué es un modelo de Markov en primer lugar. Aquí crearé un ejemplo simple utilizando dos elementos que son muy familiares en probabilidad: dados y bolsas de bolas de colores.
Los componentes del modelo, que utilizará para crear el modelo aleatorio, son:
- Un dado rojo de seis caras.
- Un dado negro de diez caras.
- Una bolsa roja con diez bolas. Nueve bolas son rojas, una es negra.
- Una bolsa negra con veinte bolas. Una bola es roja, diecinueve son negras.
“Negro” y “Rojo” son los dos estados en este modelo (en otras palabras, puedes ser negro o puedes ser rojo).
Ahora cree el modelo siguiendo estos pasos:
- PASO DE EMISIÓN: Lanza un dado. Tenga en cuenta el número que aparece. Esta es la emisión . En el gráfico anterior, elegí un dado rojo para comenzar (arbitrario, podría haber elegido el negro) y saqué 2.
- PASO DE TRANSICIÓN : Elija al azar una bola de la bolsa con el color que coincida con el dado que lanzó en el paso 1. Lancé un dado rojo, así que elegiré una bola de la bolsa roja. Saqué una bola negra, así que voy a hacer la transición al dado negro para la próxima emisión.
Luego puede repetir estos pasos para un cierto número de emisiones. Por ejemplo, repetir esta secuencia de pasos 10 veces podría darte el conjunto {2,3,6,1,1,4,5,3,4,1}. El proceso de transición de un estado al siguiente se llama proceso de Markov .
La transición de rojo a negro o de negro a rojo conlleva diferentes probabilidades ya que hay diferentes cantidades de bolas negras y rojas en las bolsas. El siguiente diagrama muestra las probabilidades de este modelo en particular, que tiene dos estados (negro y rojo):
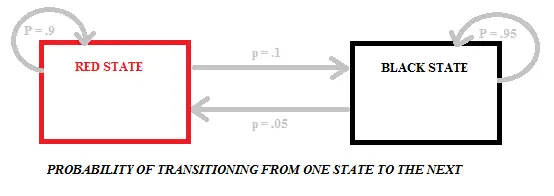
Notación del modelo oculto de Markov
λ = (A,B,π), es una notación abreviada para un HMM. En los modelos ocultos de Markov se utiliza otra notación:
- A = probabilidades de transición de estado (a ij )
- B = matriz de probabilidad de observación (b j (k))
- N = número de estados en el modelo {1,2…N} o el estado en el tiempo t →s t
- M = número de símbolos de observación distintos por estado
- Q = {q0, q1, . . . , qN−1} = estados distintos del proceso de Markov
- T = longitud de la secuencia de observación
- V = {0, 1, . . . , M − 1} = conjunto de posibles observaciones
- O = (O 0 , O 1 , . . . , O T −1 ) = secuencia de observación
- π = distribución de estado inicial (π i )
- s = estado o secuencia de estados (s 1 , s 2 … s n )
- x k = estado oculto
- zk = observación.
Tres problemas básicos
Tres problemas básicos se pueden resolver con modelos ocultos de Markov:
- Dado el Modelo Oculto de Markovλ = (A, B, π) y una secuencia de observaciones O, encuentre la probabilidad de una observación P(O | λ). Esto a veces se llama el Problema de Evaluación .
- Dado el Modelo Oculto de Markovλ = (A, B, π) y una secuencia de observación O, encuentre la secuencia de estado más probable (s 1 , s 2 … s n ). Esto a veces se denomina problema de decodificación.
- Encuentre una secuencia de observación (O 1 , O 2 …O n y modelo oculto de Markov λ = (A, B, π) que maximice la probabilidad de O. Esto a veces se denomina problema de aprendizaje o problema de optimización .
Referencias:
Rabiner, LR » Un tutorial sobre modelos ocultos de Markov y aplicaciones seleccionadas en reconocimiento de voz» , Actas del IEEE, vol. 77, pp. 257-286, febrero de 1989.
Stamp, M. (2013). Una introducción reveladora a los modelos ocultos de Markov. Recuperado el 6/8/2013 de: http://www.cs.sjsu.edu/~stamp/RUA/HMM.pdf
