Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 27 de agosto de 2021, por Luis Benites.
¿Qué es la Distribución Gaussiana Inversa?
La Distribución Gaussiana Inversa , también llamada Wald o Gaussiana normal-inversa , es una distribución exponencial con un solo modo y cola larga . La distribución se utiliza para modelar datos no negativos con sesgo positivo y tiene una amplia variedad de aplicaciones en negocios, análisis de supervivencia, finanzas, medicina e incluso en la resolución de conflictos laborales. La cola de la distribución disminuye lentamente en comparación con la distribución normal . Por lo tanto, es adecuado para modelar fenómenos en los que existe una mayor probabilidad de obtener valores extremadamente grandes en comparación con la distribución normal.
El «inverso» en el nombre es engañoso; en realidad no se refiere a la inversa de una distribución. Originalmente desarrollado para la teoría del movimiento browniano (los movimientos aleatorios de las partículas en un líquido), obtuvo el nombre de Gaussiana inversa en 1956, cuando Tweedie notó que existe una relación inversa entre la distancia recorrida en la unidad de tiempo y el tiempo para cubrir una unidad de distancia.
Función de densidad de probabilidad
La función de densidad de probabilidad para la distribución es: Donde:
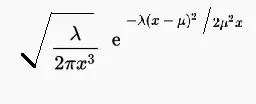
- μ un parámetro de ubicación (la media ) y
- λ un parámetro de escala .
Ambos parámetros deben ser números positivos.
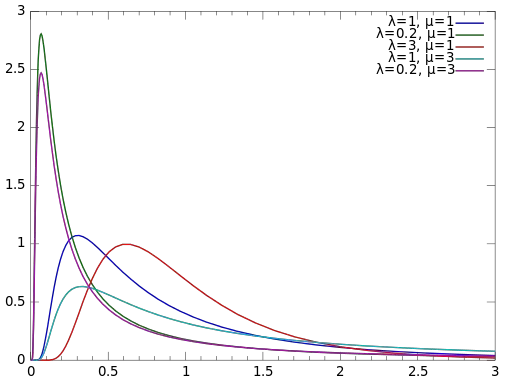
PDF para la Gaussiana Inversa.
Similitudes con otras distribuciones
Aunque la distribución gaussiana inversa a veces se denomina distribución «normal inversa», no debe confundirse con la distribución normal inversa , que es una forma de encontrar probabilidades para una distribución normal.
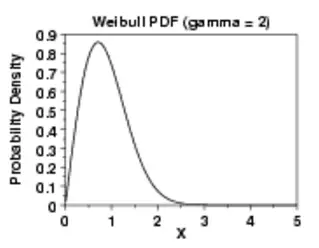
Esta distribución tiene una forma similar a la distribución Weibull , pero tiene la ventaja de que es más fácil estimar probabilidades (la Weibull, con tres parámetros, es más difícil).
La distribución Gamma también tiene una forma similar. De hecho, pueden verse exactamente iguales con los parámetros correctos. Sin embargo, es más fácil producir valores extremadamente grandes con la Gaussiana inversa.
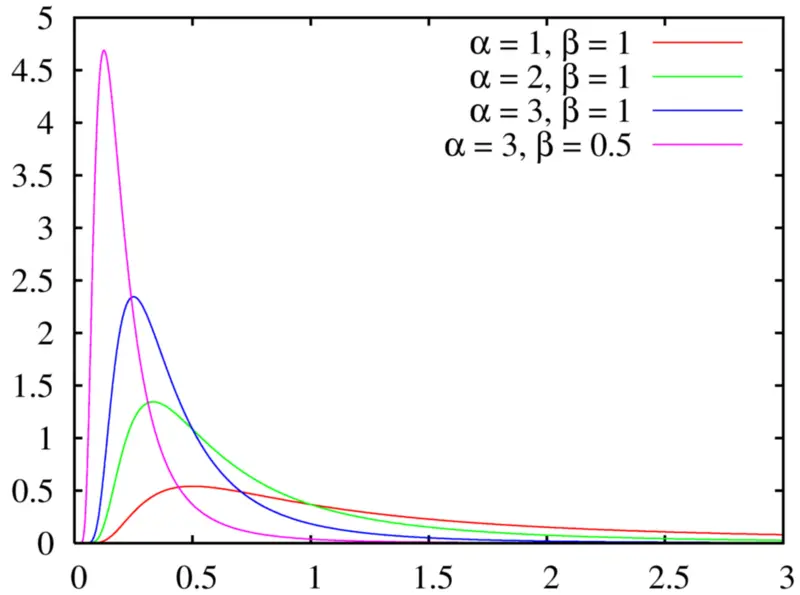
La familia de distribución gamma.
Referencias:
Schrodinger E., 1915, Zur Theorie der Fall-und Steigversuche an Teilchen mit Brownscher Bewegung, Physikalische Zeitschrift 16, 289–295.
Tweedie, MCK (1956). Algunas propiedades estadísticas de las distribuciones gaussianas inversas. Revista de Ciencias de Virginia, 7, 160-165.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
