Intervalo de confianza asintótico

Actualizado el 1 de marzo de 2022, por Luis Benites.

El intervalo de confianza asintótico es el método de «libro de texto» para construir intervalos de confianza. Es válido para tamaños de muestra grandes (de ahí el nombre alternativo, intervalo de confianza de «muestra grande»), pero no existen pautas establecidas sobre qué tan grande es «suficientemente grande» [1]. Si conoce la distribución de su estadística , puede construir un intervalo de confianza exacto. Sin embargo, en la mayoría de los casos, no conoce la distribución exacta, por lo que debe crear un intervalo de confianza aproximado, uno asintótico.

Intervalo de confianza exacto vs. asintótico

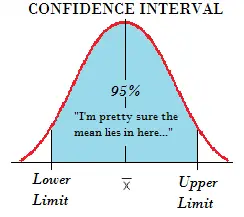
Un nivel de confianza nos dice qué tan seguros estamos de que nuestros resultados contienen el verdadero parámetro de población.

Cuando se conoce la distribución exacta de una estadística, la probabilidad de cobertura (la probabilidad de que el intervalo aleatorio incluya el parámetro de población real) es igual al nivel de confianza y el intervalo de confianza es exacto. En otras palabras, un intervalo de confianza exacto dará el nivel de confianza exacto establecido (por ejemplo, 95%); Está garantizado que si tuviera que repetir un experimento o una encuesta una y otra vez, el 95% de las veces obtendría los mismos resultados.
Por otro lado, un intervalo de confianza asintótico solo dará una aproximación. Por ejemplo, en lugar del 95 %, en realidad podría obtener el 91 %. Una forma de lidiar con esto es usar los intervalos de confianza de Wilson , que tienen mejores tasas de cobertura para muestras pequeñas.

No existe una “manera correcta” de construir un intervalo de confianza asintótico. Sin embargo, cuanto mayor sea su muestra, mejor. Los métodos para encontrar intervalos de confianza asintóticos incluyen estimadores de máxima verosimilitud , transformación Z y el procedimiento de estudentización [2].

Referencias