Actualizado por ultima vez el 6 de septiembre de 2021, por Luis Benites.
Nota : para comprender la prueba de White, es posible que desee leer primero este artículo sobre heteroscedasticidad .
¿Qué es la Prueba Blanca?
La prueba de White se usa para probar los errores heteroscedásticos («diferentemente dispersos») en el análisis de regresión . Es un caso especial de la prueba (más simple) de Breusch-Pagan .
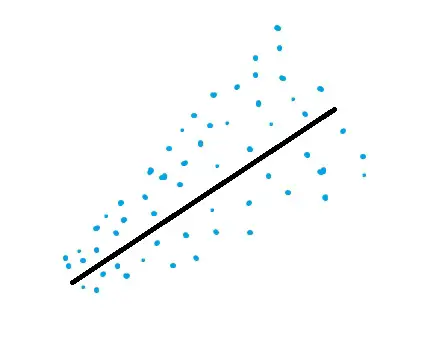
Un gráfico que muestra la heterocedasticidad; la prueba de White se utiliza para identificar errores heteroscedásticos en el análisis de regresión.
La hipótesis nula de la prueba de White es que las varianzas de los errores son iguales. En términos matemáticos, eso es:
H 0 = σ 2 i = σ 2 .
La hipótesis alternativa (la que está probando) es que las varianzas no son iguales:
H 1 = σ 2 i ≠ σ 2 .
La única diferencia entre la prueba de White y la de Breusch-Pagan es que su regresión auxiliar no incluye términos cruzados ni las variables cuadradas originales. Aparte de eso, los pasos son exactamente los mismos.
¿Cuándo debe usar la prueba de White?
Si su conjunto de datos tiene muchas variables explicativas , la prueba puede ser difícil de calcular. A menos que tenga una razón específica para ejecutar la prueba de White (es decir, necesita que su variable independiente tenga un efecto no lineal interactivo en la varianza), debe usar el Breusch-Pagan más simple. La prueba de White es una prueba asintótica , que está destinada a usarse en muestras grandes. Para muestras más pequeñas, interprete los resultados con precaución.
Un problema con la prueba de White es que puede arrojar un resultado significativo incluso si las varianzas de los errores son iguales. Esto sucede porque el modelo es general y puede detectar otros problemas en sus datos (¡aunque no especificará cuáles son esos problemas!). Según Richard Williams, una de las razones por las que la prueba es más general es por los términos agregados que prueban más tipos de heteroscedasticidad, como agregar cuadrados de regresores (es decir, las variables independientes) para tratar de identificar formas no lineales como un reloj de arena.
Referencias
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Blanco, H. (1980). “Un estimador de matriz de covarianza consistente con heterocedasticidad y una prueba directa para heterocedasticidad”. Econométrica. 48 (4): 817–838
Williams, R. Recuperado el 27 de junio de 2016 de: https://www3.nd.edu/~rwilliam/stats2/l25.pdf.

