Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 8 de febrero de 2022, por Luis Benites.
¿Qué es la prueba del punto de inflexión?
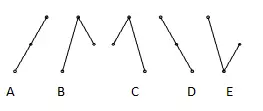
B, C y E tienen puntos de inflexión (ya sea picos o valles).
La prueba del punto de inflexión es una prueba que nos permite comprobar si un conjunto de variables aleatorias son independientes e idénticamente distribuidas.
Propuesta por Irénée-Jules Bienaymé en 1874, esta prueba sigue siendo una parte importante de la caja de herramientas estadísticas. En aplicaciones científicas, se usa más comúnmente para encontrar si un conjunto de datos de series temporales es verdaderamente aleatorio.
Una comprensión intuitiva de la prueba del punto de inflexión
Para comprender la idea detrás de esta prueba, considere un conjunto de tres puntos. Si el punto medio está por encima o por debajo de los otros dos, hay un punto de inflexión . Un conjunto de datos de observación donde cada observación es un poco mayor que la siguiente no tendría ningún punto de inflexión. Tal conjunto fallaría la prueba del punto de inflexión para la aleatoriedad.
Si tiene una serie aleatoria de n períodos de duración, puede esperar que el número de puntos de inflexión sea aproximadamente: 
La varianza en el número de puntos de inflexión sería:
.
A medida que aumenta el número de puntos de datos, la distribución del número de puntos de inflexión se acerca rápidamente a la normalidad . Para una serie de n puntos, debe haber alrededor de
(2/3)(n − 2)
puntos de inflexión. A medida que n crece, debería tener alrededor de
N(2n/3, 8n/45)
puntos. En el nivel alfa
del 5% , puede rechazar la hipótesis nula de que la serie es aleatoria si el número de puntos se encuentra fuera del rango 2n/3 ± 1,96 √8n/45.
Lo que esto significa es que una mirada a la cantidad de puntos de inflexión es una forma muy efectiva de marcar datos no aleatorios. La prueba del punto de inflexión es una prueba especialmente buena para descubrir la ciclicidad . No es tan útil para descartar tendencias generales.
La estadística de prueba del punto de inflexión
Para aplicar la prueba del punto de inflexión a un conjunto de datos, donde n > 15, deje que su hipótesis nula sea que son variables aleatorias distribuidas de manera independiente e idéntica. Entonces puedes calcular el valor de
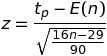Donde t p es el número de puntos de inflexión (picos y valles) y
.
Este estadístico de prueba tiene una distribución normal .
Referencias
Nielsen, A. (2019). Análisis Práctico de Series Temporales: Predicción con Estadística y Aprendizaje Automático 1ª Edición. O´Reilly Media.
Stoffer, D. (2017). Análisis de series temporales y sus aplicaciones: con ejemplos de R 4ª ed . Saltador.
Universidad de Cambridge. Series de tiempo.
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
