Pruebas de razón de verosimilitud (probabilidad y estadística matemática)

Actualizado el 13 de octubre de 2021, por Luis Benites.

Este artículo trata sobre las pruebas de razón de verosimilitud utilizadas en probabilidad y estadística matemática . Si buscas información sobre el cociente que se utiliza para evaluar las pruebas diagnósticas en medicina, consulta este otro artículo: ¿Qué es un Cociente de Verosimilitud?

¿Qué es una prueba de razón de verosimilitud?

La prueba de razón de verosimilitud (a veces llamada prueba de chi-cuadrado de razón de verosimilitud) es una prueba de hipótesis que le ayuda a elegir el «mejor» modelo entre dos modelos anidados . “Modelos anidados” significa que uno es un caso especial del otro. Por ejemplo, es posible que desee averiguar cuál de los siguientes modelos es el más adecuado:

• El modelo uno tiene cuatro variables predictoras (altura, peso, edad, sexo),
• El modelo dos tiene dos variables predictoras (edad, sexo). Está «anidado» dentro del modelo uno porque tiene solo dos de las variables predictoras (edad, sexo).

Esta teoría también puede aplicarse a matrices . Por ejemplo, una matriz de identidad escalada se anida dentro de una matriz de simetría compuesta más compleja.

El mejor modelo es el que hace que los datos sean más probables, o maximiza la función de verosimilitud “>función de verosimilitud , f _n (X – 1, …, X _n |Θ).
Aunque el concepto es relativamente fácil de comprender (es decir, la función de verosimilitud es más cercana al valor real de Θ), los cálculos para encontrar las entradas del procedimiento no lo son.

Las pruebas de razón de verosimilitud usan funciones logarítmicas de verosimilitud , que son difíciles y largas de calcular a mano. La mayoría de los paquetes de software estadístico tienen funciones integradas para manejarlos; Por otro lado, las funciones logarítmicas de verosimilitud plantean otros serios desafíos, como la dificultad de calcular máximos globales . Estos a menudo implican cálculos pesados ​​con integrales multidimensionales complicadas .

Ejecución de la prueba

Básicamente, la prueba compara el ajuste de dos modelos. La hipótesis nula es que el modelo más pequeño es el «mejor» modelo; Se rechaza cuando el estadístico de prueba es grande. En otras palabras, si se rechaza la hipótesis nula , entonces el modelo más grande es una mejora significativa sobre el más pequeño.

Si conoce las funciones de log-verosimilitud para los dos modelos, la estadística de prueba es relativamente fácil de calcular como la relación entre la log-verosimilitud del modelo (s) más simple (s) y el modelo con más parámetros (g): También puede ver esta ecuación con «s» escrita como la probabilidad del modelo nulo y «g» escrita como la probabilidad del modelo alternativo.

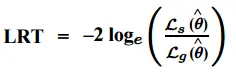
La estadística de prueba se aproxima a una variable aleatoria de chi-cuadrado . Los grados de libertad de la prueba equivalen a la diferencia en el número de parámetros de los dos modelos.