Actualizado por ultima vez el 30 de noviembre de 2021, por Luis Benites.
La regla empírica del rango es un método útil para estimar el rango a partir de la desviación estándar . Nos dice que el rango es generalmente alrededor de cuatro veces la desviación estándar.
Entonces, si su desviación estándar es 2, puede suponer que su rango es aproximadamente ocho.
Usando la regla general del rango, también es posible estimar una desviación estándar cuando se conoce el rango. Simplemente divida el rango por cuatro.
La regla general del rango funciona mejor para los datos de una distribución normal donde el tamaño de la muestra es cercano a treinta. Para muestras que son mucho más pequeñas o mucho más grandes que treinta, o que no siguen la distribución normal, puede ser una muy mala suposición.
Reglas alternativas
Hay ‘reglas generales’ alternativas que tienden a proporcionar mejores conjeturas, pero también son mucho más pesadas en el cálculo. Por ejemplo, una sugerencia de Ramirez y Cox (2012) para una regla es la siguiente: la fórmula se limita a la distribución normal, pero los autores ofrecen sugerencias para otras distribuciones. Puedes encontrar su artículo aquí .
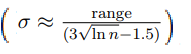
Otros usos de la regla práctica del rango
La regla general del rango sugiere que la mayoría de los valores estarían en el área cubierta por cuatro desviaciones estándar: es decir, dentro de dos desviaciones estándar por encima o por debajo de la media . Esto nos permite definir valores inusuales como aquellos que no caen dentro de este rango. Llamamos al valor habitual máximo la media más dos desviaciones estándar, y al valor habitual mínimo la media menos dos desviaciones estándar.
Referencias
Ramírez, Alfredo. Cox, Carlos. Mejorando la regla empírica del rango. Rose Hulman Undergraduate Mathematics Journal, Volumen 13, No. 2, otoño de 2012. Obtenido de https://scholar.rose-hulman.edu/cgi/viewcontent.cgi?article=1211&context=rhumj el 28 de agosto de 2018.
Triola, MF Estadística elemental usando Excel. Sección 5-2, Variables aleatorias. Recuperado de http://math.tntech.edu/e-stat/TRIOLA/Chapter5.pdf el 28 de agosto de 2018.
Jones, James. Medidas de varianza. Recuperado de https://people.richland.edu/james/ictcm/2001/descriptive/helpvariance.html el 28 de agosto de 2018.
Tanbakuchi, Anthony. Conferencias introductorias de estadística: medidas de variación. Departamento de Matemáticas, Pima Community College. Recuperado de http://www.u.arizona.edu/~kuchi/Courses/MAT167/Files/LH_LEC.0230.DescStats.Variation.pdf el 28 de agosto de 2018.

