Contenido de este artículo
- 1 Supuestos y condiciones para la regresión.
- 2 La Condición de Datos Cuantitativos/Condición de Variables Cuantitativas.
- 3 Variables categóricas que se disfrazan de cuantitativas.
- 4 La Condición Suficientemente Recta (Asunción de Linealidad).
- 5 La condición atípica.
- 6 Independencia de errores
- 7 homocedasticidad
- 8 Normalidad de la distribución de errores
- 9 Redactor del artículo
- 10 ¿Te hemos ayudado?
Actualizado el 9 de diciembre de 2021, por Luis Benites.
Supuestos y condiciones para la regresión.
La regresión puede ser una herramienta muy útil para encontrar patrones en conjuntos de datos. Sin embargo, sus datos no siempre se pueden ajustar a una línea de regresión. La mayoría del software, como SPSS y Excel , siempre le dará la mejor línea de regresión que pueda encontrar , incluso si la línea de regresión no tiene sentido. Depende de usted determinar de antemano si sus datos tienen sentido para el análisis de regresión. ¿Cómo haces eso? Al considerar las siguientes suposiciones y condiciones para la regresión antes de ejecutar la prueba:
- La condición de datos cuantitativos.
- La Condición Suficientemente Recta (o “linealidad”).
- La condición atípica.
- Independencia de errores
- homocedasticidad
- Normalidad de la distribución de errores
Mire el video para obtener una descripción general:
Supuestos y condiciones para la regresión Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
La Condición de Datos Cuantitativos/Condición de Variables Cuantitativas.
Solo puede realizar regresiones en variables cuantitativas . En otras palabras, si sus datos no son un conjunto de números, la regresión no es un buen método para encontrar una tendencia . Verifique que sus variables tengan unidades reales y que estén midiendo algo que tenga sentido.
Para saber si sus datos cumplen con la condición de datos cuantitativos, debe asegurarse de tener datos cuantitativos (datos numéricos ) y no datos cualitativos. Los datos cualitativos son datos que encajan en categorías (por eso también se les llama datos categóricos ). Ver: Cuantitativo o Cualitativo: Cómo Clasificar Variables .
Variables categóricas que se disfrazan de cuantitativas.
 A veces, en estadísticas, puede asignar números a variables categóricas para obligarlas a convertirse en cuantitativas (para que pueda realizar cálculos). Por ejemplo, una baraja de cartas se compone de variables cuantitativas (los números de las cartas) y variables categóricas (los palos: corazones, diamantes, picas, tréboles). Puedes dar números a los palos para que sean numéricos:
A veces, en estadísticas, puede asignar números a variables categóricas para obligarlas a convertirse en cuantitativas (para que pueda realizar cálculos). Por ejemplo, una baraja de cartas se compone de variables cuantitativas (los números de las cartas) y variables categóricas (los palos: corazones, diamantes, picas, tréboles). Puedes dar números a los palos para que sean numéricos:
- Corazones = 1
- Diamantes = 2
- Picas = 3
- clubes = 4
Sin embargo, dar números a datos categóricos no los convierte en variables cuantitativas; Todavía son variables categóricas: solo aquellas a las que se les han asignado números. Por lo tanto, no puede realizar una regresión en este tipo de variables porque no cumplen con la condición de variables cuantitativas.
La Condición Suficientemente Recta (Asunción de Linealidad).
( Solo regresión lineal ). Las líneas de regresión serán muy engañosas si sus datos no son aproximadamente lineales. La mejor manera de verificar esta condición es hacer un diagrama de dispersión de sus datos. Si parece que los datos caben aproximadamente en una línea, puede realizar una regresión. Para otros tipos de regresión (como la regresión exponencial ), observa el diagrama de dispersión para asegurarte de que sigue aproximadamente la forma de cualquier regresión que estés realizando.
La condición atípica.
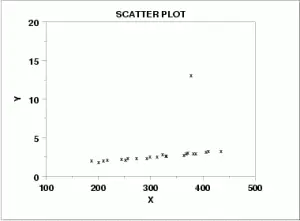
Un valor atípico puede afectar dramáticamente su línea de regresión.
Los valores atípicos pueden tener un efecto dramático en las líneas de regresión y el coeficiente de correlación que obtiene cuando ejecuta el análisis de regresión. Si tiene un valor atípico en sus datos, es una buena idea ejecutar el análisis de regresión dos veces: una vez con el valor atípico y otra sin él.
Independencia de errores
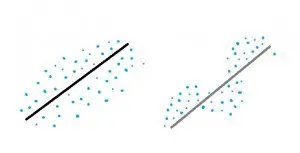
Si sus puntos siguen un patrón claro, podría indicar que los errores se están influenciando entre sí. Los errores son las desviaciones de un valor observado del valor real de la función. La siguiente imagen muestra dos líneas de regresión lineal; a la izquierda, los puntos están dispersos al azar. A la derecha, los puntos se influyen claramente entre sí. Si no tiene errores aleatorios, no puede ejecutar una regresión lineal ya que sus predicciones no serán precisas.
homocedasticidad
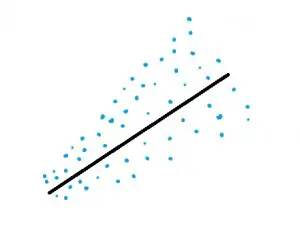
Con la homocedasticidad, básicamente quieres que tus puntos se vean como un tubo en lugar de un cono. La heterocedasticidad es donde, como la independencia de los errores, se ve una tendencia en los errores, pero esta vez la tendencia es mayor o menor (a diferencia de los errores que claramente se influyen entre sí). En la imagen de abajo, el gráfico de la izquierda muestra una línea de regresión lineal donde los errores son cada vez mayores. La forma es como un cono. Ejecutar una regresión lineal en datos que muestran heterocedasticidad le dará resultados deficientes.
Normalidad de la distribución de errores
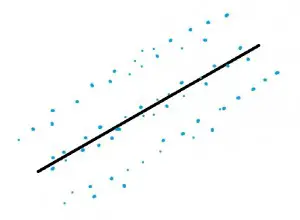
En cualquier punto de los valores de x, los puntos de datos deben distribuirse normalmente alrededor de la línea de regresión. Sus valores deben estar bastante cerca de la línea, distribuidos uniformemente con solo unos pocos valores atípicos. La siguiente imagen muestra datos que se distribuyen de manera bastante normal a la izquierda. Los datos de la derecha tienen datos que están agrupados en la línea o lejos de la línea. La regresión lineal no debe ejecutarse en valores que no se distribuyen normalmente.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
