Actualizado por ultima vez el 27 de octubre de 2021, por Luis Benites.
¿Qué es el Centro de una Distribución?
El centro de una distribución es el medio de una distribución . Por ejemplo, el centro de 1 2 3 4 5 es el número 3. Por supuesto, no suele ser tan fácil. Si se le pide que encuentre el centro de una distribución en estadísticas, generalmente tiene tres opciones:
- Mire un gráfico o una lista de números y vea si el centro es obvio.
- Encuentre la media , el “ promedio ” del conjunto de datos.
- Encuentra la mediana , el número del medio.
No hay una forma correcta de definir el «medio». Si se le pide que encuentre el centro de una distribución y no está seguro de lo que se supone que debe encontrar, lo más seguro es consultar con su instructor para averiguar qué centro se supone que debe encontrar. Si eso no es posible, la respuesta más probable es mirar un gráfico y mirar el centro. Por ejemplo, el siguiente gráfico muestra la barra central resaltada: Si tiene números reales, tendrá que elegir si desea que la media o la mediana sean el centro de una distribución. En general: use la media si no tiene valores atípicos (valores muy bajos o muy altos) y use la mediana si tiene valores atípicos o si su gráfico está muy sesgado .
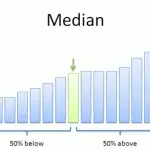
.
Centro de un ejemplo de distribución
El siguiente diagrama de tallo muestra el porcentaje de residentes de 65 años o más en los Estados Unidos (según el censo de 2000). Los tallos son porcentajes enteros y las hojas son décimas de un por ciento. Encuentre el centro de la distribución.
Tallos = porcentajes enteros
Hojas = décimas de un por ciento
6 8
7
8 8
9 79
10 08
11 15566
12 012223444457888999
13 01233333444899
14 02666
15 23
16 8
Hay varias formas de abordar este problema. En primer lugar, podría simplemente mirar el diagrama de tallo y ver que la mayor parte de los datos se encuentran en el medio, la columna del 12 por ciento, por lo que podría decir que ese es el centro de esta distribución en particular. Si quiere probarlo matemáticamente, encuentre la media:
Paso 1: Escriba el número del diagrama de tallo. Si no está seguro de cómo hacerlo, le recomendamos que consulte este artículo: Stemplot en estadísticas.
6,8
8,8
9,7 9,9
10,0 10,8
11,1 11,5 11,5 11,6 11,6
12,0 12,1 12,2 12,2 12,2 12,3 12,4 12,4 12,4 12,4 12,5 12,7 12,8 12,8 12,8 12,9 12,9 12,9
13,0 13,1 13,2 13,3 13,3 13,3 13,3 13,3 13,4 13,4 13,4 13,8 13,9 13,9
14,0 14,2 14,6 14,6 14,6
15.2 15.3
16.8
Paso 2: Calcule la media sumando todos los números y dividiendo por el número de artículos en el conjunto (que es 50):
8.8+ 9.7+ 9.9+ 10.0 +10.8+ 11.1+ 11.5+ 11.5+ 11.6+ 11.6 + 12.0+ 12.1+ 12.2+ 12.2+ 12.2+ 12.3+ 12.4+ 12.4+ 12.4+ 12.4+ 12.5+ 12.7+ 12.8+ 12.8+ 12.8+ 12.9+ 12.9+ 12.9+ 13.0 +13.1 +3 +3.3 +13.3 +3.3 +13.2 +1 + 13.3+ 13.4+ 13.4+ 13.4+ 13.8+ 13.9+ 13.9+ 14.0+ 14.2+ 14.6+ 14.6+ 14.6+ 15.2+ 15.3+ 16.8 = 638.3
Entonces: 638.3 / 50 = 12.766
También puedes encontrar la mediana. El medio de un conjunto de 50 números es el número 25, que es 12,8.
Tenga en cuenta que la media, 12.766 y la mediana, 12.8 caen en el percentil 12, que es donde supusimos que estaba el centro de la distribución con solo mirarlo.
¡ Visite nuestro canal de YouTube para ver cientos de videos de ayuda sobre estadísticas!

