Actualizado por ultima vez el 16 de mayo de 2022, por Luis Benites.
¿Qué es un Stemplot?
Un diagrama de tallo es como un histograma : ambas son herramientas que lo ayudan a visualizar un conjunto de datos . Los diagramas de tallo muestran un poco más de información que un histograma y han sido una herramienta común para mostrar conjuntos de datos desde la década de 1970. Suelen utilizarse cuando hay una cantidad media de variables cuantitativas para analizar; Los gráficos de tallo de más de 50 observaciones son inusuales. El nombre «Gráfica de tallo» viene porque hay un «tallo» con los dígitos de valor posicional más grandes a la izquierda (sombreados en gris en la imagen de abajo) y una «hoja» a la derecha. Los primeros valores de este diagrama de tallo son: 21 24 25 25 26 (la primera línea). 31 32 32 37 (la segunda línea)


¿Para qué se utilizan los Stempllots?
Un diagrama de tallo y hojas es una forma de graficar datos donde los datos se dividen en tallos (el dígito más grande) y hojas (los dígitos más pequeños). Fueron ampliamente utilizados antes de la llegada de la computadora personal , ya que eran una forma rápida de dibujar distribuciones de datos a mano. Se usan con menos frecuencia hoy en día, pero aún verá algunos aquí y allá.
El diagrama de tallo y hoja se usa como un histograma; le permite comparar datos . Mientras que un histograma usa barras para representar cantidades, las hojas del diagrama de tallo representan cantidades. Una hoja muy larga significa que el “tallo” tiene una gran cantidad de datos. Los tallos con la mayor cantidad de datos en la imagen de arriba son los tallos 2 y 6.
Los números están ordenados por valor posicional. Los dígitos de valor posicional más grandes se colocan en la raíz. Los diagramas de tallo en el mundo real no suelen estar etiquetados con los valores posicionales que representa el tallo; por lo general, depende de usted averiguarlo en función del contexto y los datos. Sin embargo, en los libros de texto y otros materiales educativos, es común que los diagramas de tallo estén etiquetados. Por ejemplo, una clave al lado del siguiente diagrama de tallo le dice que 7|5 significa 75, lo que indica que el tallo representa decenas y la hoja representa unidades. Los valores de los tallos se enumeran hacia abajo (en orden ascendente, de menor a mayor) y los valores de las hojas se enumeran de derecha a izquierda (en orden ascendente, de menor a mayor).

Ventajas
Los diagramas de tallo y hoja son útiles en algunos casos porque puede ver dónde se encuentra la mayor parte de las puntuaciones. En el gráfico anterior, la mayoría de las puntuaciones estaban entre los 20 y los 60 años. Los gráficos de barras también muestran esta información, pero la ventaja que tienen los diagramas de tallo y hoja es que puedes ver todas las puntuaciones (otros gráficos generalmente muestran solo los totales). Estos tipos de gráficos le brindan una descripción general rápida de una distribución y también puede ver la forma de la distribución (piense en cada hoja como si representara una barra en un gráfico de barras ). También son útiles para resaltar la moda (el número más común en un conjunto de datos) y para encontrar valores atípicos .
Desventajas
Una desventaja de los diagramas de tallo y hoja es que en realidad solo son útiles para pequeños conjuntos de datos de alrededor de 15 a 150 puntos de datos. Los diagramas de puntos suelen ser más útiles para conjuntos de datos más pequeños, y para conjuntos de datos más grandes se usa un diagrama de caja o un histograma .
Stempllots espalda con espalda
Los tallos espalda con espalda tienen dos hojas que comparten un solo tallo. El tallo en el diagrama de tallos adosado está sombreado en gris en la siguiente imagen.
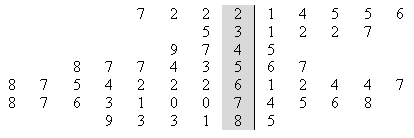
¿Qué significa recortar las hojas en un tallo?
Recortar las hojas significa deshacerse de dígitos innecesarios en sus datos. Digamos que estaba trazando los siguientes números en un diagrama de tallo:
141 162 112 153 137 106 103 82 151
Para estos números, desearía que el tallo fuera el dígito del lugar de las centenas y las hojas el lugar de las decenas. Eso hace que las unidades sean innecesarias, así que recórtelas (redondéelas) para obtener:
140 160 110 150 130 100 100 80 150
¿Qué significa dividir el tallo en un Stempllot?
Digamos que tiene este conjunto de datos para el que desea hacer un diagrama de tallo:
140 160 110 150 130 100 100 80 150
170 200 170 100 170 360 150 150 260
Los tallos en este diagrama de tallo serían los dígitos de las centenas (0,1, 2,3). Eso le daría un tallo muy pequeño con solo cuatro tallos.
0
1
2
3
Lo ideal es tener entre 6 y 20 tallos en una parcela. Solo tenemos cuatro, así que divide los tallos en dos para obtener ocho tallos. La primera parte de la potencia dividida se puede utilizar para 0-49 y la segunda parte de la potencia para 50-99. Así es como se ingresarían los números 140 160 110 150 y 130 en este diagrama de tallo:
0
0
1 | 4 1 3
1 | 6 5
2
2
3
3
Cómo hacer un diagrama de tallo
Los diagramas de tallo se componen de un tallo (generalmente el dígito de valor posicional más alto) y «hojas», que son los dígitos o unidades. Por ejemplo, un diagrama de tallo simple de 10,21 y 32 tendría decenas como dígitos de mayor orden y 0,1 y 2 como hojas. Piense en un diagrama de tallo como un histograma o gráfico de barras hecho de números reales en lugar de bloques.
Pregunta de ejemplo: haga un gráfico de tallo a partir del siguiente conjunto de datos, que representa los puntajes de las pruebas de tercer grado: 64, 82, 85, 99, 96, 81, 97, 80, 81, 80, 84, 87, 98, 75, 86, 88 , 82, 78, 81, 86, 80, 50, 84, 88, 83, 82.
Paso 1: Ordena los números de menor a mayor: 50, 64, 75, 78, 80, 80, 80, 81, 81, 81, 82, 82, 82, 83, 84, 84, 85, 86, 86 , 87, 88, 88, 96, 97, 98, 99.
Paso 2: elige tu potencia. Generalmente, el tallo será el valor posicional más grande. Para este conjunto de datos, el valor posicional más grande es 10, por lo que el tallo de esta pregunta de muestra representará las unidades de las decenas.
Paso 3: separe sus números ordenados (del Paso 1) en grupos según el valor posicional que eligió en el Paso 2. Para esta pregunta de muestra, elegimos las decenas como el valor posicional, por lo que los grupos son:
50
64
75, 78
80, 80, 80, 81, 81, 81, 82, 82, 82, 83, 84, 84, 85, 86, 86, 87, 88, 88
96, 97, 98, 99.
Aunque no es estrictamente necesario, este paso facilita la visualiza el diagrama de tallo y hojas uniéndose.
Paso 4: Dibuja un contorno de tu gráfico. Todo lo que realmente se necesita para hacer un diagrama de tallo simple es una línea vertical:

Paso 5: Dibuja los números de los tallos. Para este problema de muestra, el tallo representa decenas. Los puntajes van de 50 a 99, por lo que las decenas son 5, 6, 7, 8 y 9.

Paso 6: Dibuja los dígitos de las hojas según las agrupaciones del Paso 3 . Estos son los dígitos de las hojas en negrita, junto con el diagrama de tallo terminado:
5 0
6 4
7 5 , 7 8
8 0 , 8 0 , 8 0 , 8 1 , 8 1 , 8 1 , 8 2 , 8 2 , 8 2 , 8 3 , 8 4 , 8 4 , 8 5 , 8 6 , 8 6 , 8 7 , 8 8 , 8 8
9 6 , 9 7 , 9 8 , 9 9

¡Así es como se hace un diagrama de tallo, de la manera más fácil!
Referencias
Moore, D. y Notz, W. (2019). Estadística: Conceptos y Controversias . WH Freeman.

