Actualizado por ultima vez el 12 de enero de 2022, por Luis Benites.
¿Qué es un Coeficiente de Dispersión (COD)?
El término «coeficiente de dispersión» puede significar algunas cosas diferentes en estadística. No hay una fórmula o definición que sea universal. Todo depende del contexto en el que estés usando el coeficiente y lo que quieras hacer con él:
- De manera informal, algunas personas usan «coeficiente de dispersión» de manera intercambiable con «coeficiente de variación» .
- El coeficiente de dispersión de Karl Pearson es simplemente la relación entre la desviación estándar y la media .
- La DQO de Green (C x ) es adecuada cuando se trata de densidades. La fórmula es: varianza muestral / media muestral – 1/Σ(x-1).
- Como medida de dispersión alrededor de una mediana , puede usar la fórmula:
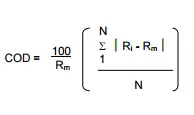
Donde:
R m = relación mediana;
R i = relación observada.
N = número en la muestra.
Esto se usa casi exclusivamente para tratar con valores de propiedad y de mercado. Para conocer los pasos de la solución, consulte esta hoja del gobierno del estado de Nueva York . - El coeficiente de dispersión del cuartil (ver más abajo), que es una de las versiones más populares de COD encontradas en la investigación.
¿Qué es un coeficiente de dispersión de cuartil?
El coeficiente de dispersión del cuartil) es una medida de la dispersión de un conjunto de datos. La fórmula es: Donde :
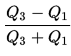
- Q 1 es el primer cuartil ,
- Q 3 es el tercer cuartil.
El CoD le dice qué tan dispersos son los conjuntos de datos entre sí. Por ejemplo, si un conjunto de datos tiene un CoD de 0,5 y otro tiene un CoD de 0,10, entonces el conjunto de datos 1 es 5 veces mayor (0,5/0,10) que el conjunto de datos 2.
Ejemplo
¿Cuál es el coeficiente de dispersión del cuartil para el siguiente conjunto de números?
2, 4, 6, 8, 10, 12, 14
Paso 1: encuentre el percentil 25 (Q 1 ) y el percentil 75 (Q 3 ). Hay algunas maneras de hacer esto. Una de las formas más sencillas es usar nuestra calculadora de rango intercuartílico . A mano, consulte: Hallar cuartiles.
Introduciendo el conjunto de datos en la calculadora, obtenemos:
- Q 1 = percentil 25 = 4
- Q 2 = percentil 75 = 12.
Paso 2: Introduce los números del Paso 1 en la fórmula y resuelve: El coeficiente de dispersión para este conjunto de datos es 0,5.
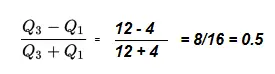
Referencias :
Bonett, DG (2006). Intervalo de confianza para un coeficiente de variación del cuartil. Estadística computacional y análisis de datos. 50 (11): 2953–2957
Verde, R. (1966). Medidas de no aleatoriedad en la distribución espacial. Res. Población Ecol. 8:1-7.
M. Kendall y A. Stuart, La teoría avanzada de la estadística, vol. 1, 4ª edición, Charles Grifin and Co.
London, (1977).

