Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 16 de marzo de 2022, por Luis Benites.
¿Qué es la prueba de Durbin Watson?
La prueba de Durbin Watson es una medida de la autocorrelación (también llamada correlación serial ) en los residuos del análisis de regresión . La autocorrelación es la similitud de una serie de tiempo en intervalos de tiempo sucesivos. Puede dar lugar a subestimaciones del error estándar y hacer que piense que los predictores son significativos cuando no lo son. La prueba de Durbin Watson busca un tipo específico de correlación serial, el proceso AR(1) .
Las hipótesis para la prueba de Durbin Watson son:
H 0 = sin autocorrelación de primer orden.
H 1 = existe una correlación de primer orden.
(Para una correlación de primer orden, el retraso es una unidad de tiempo).
Las suposiciones son:
- Que los errores se distribuyen normalmente con una media de 0.
- Los errores son estacionarios .
El estadístico de prueba se calcula con la siguiente fórmula: Donde E t son los residuos de una regresión de mínimos cuadrados ordinarios .
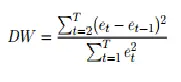
La prueba de Durbin Watson reporta una estadística de prueba, con un valor de 0 a 4, donde:
- 2 no hay autocorrelación.
- 0 a <2 es autocorrelación positiva (común en datos de series de tiempo).
- >2 a 4 es autocorrelación negativa (menos común en datos de series de tiempo).
Una regla general es que los valores estadísticos de prueba en el rango de 1.5 a 2.5 son relativamente normales. Los valores fuera de este rango pueden ser motivo de preocupación. Field (2009) sugiere que los valores por debajo de 1 o más de 3 son una causa definitiva de preocupación.
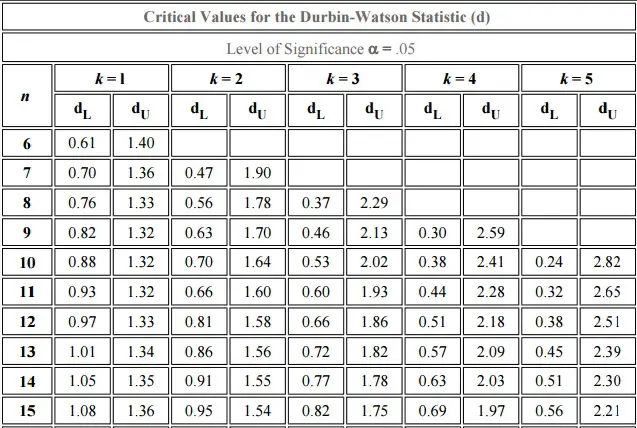
La prueba de Durbin Watson rara vez se usa y algunos la consideran arcaica. Requiere el uso de tablas, que puede encontrar principalmente en textos más antiguos. Aquí hay un extracto de una tabla (Stanford, nd) en el nivel alfa del 5% (el nivel de significación más común usado): Como las tablas son tan engorrosas, querrá usar la tecnología para encontrar la estadística DW.
Opciones de tecnología
- En Minitab:
Haga clic en Estadísticas > Regresión > Regresión > Ajustar modelo de regresión. Haga clic en «Resultados» y verifique la estadística de Durbin-Watson. - SAS: Encuentre direcciones aquí en el sitio web de UCLA .
- MATLAB: El procedimiento se puede encontrar aquí en el sitio de Mathworks .
- SPSS: en el cuadro de diálogo de regresión principal, haga clic en Estadísticas. Marque la casilla de Durbin-Watson (en la sección Residuales de Estadísticas de regresión lineal).
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Agresti A. (1990) Análisis de datos categóricos. John Wiley and Sons, Nueva York.
Esquivar, Y. (2008). La Enciclopedia Concisa de Estadística . Saltador.
Field, A. [2009], Discovering statistics using SPSS, tercera edición, Sage Publications.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
Stanford. Tabla DW recuperada el 16 de septiembre de 2020 de: http://web.stanford.edu/~clint/bench/dwcrit.htm
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
