Estacionariedad y diferenciación: definición, ejemplos, tipos

Actualizado el 25 de diciembre de 2021, por Luis Benites.

1. ¿Qué es la Estacionariedad?

Una serie de tiempo tiene estacionariedad si un cambio en el tiempo no provoca un cambio en la forma de la distribución. Las propiedades básicas de la distribución como la media , la varianza y la covarianza son constantes en el tiempo.

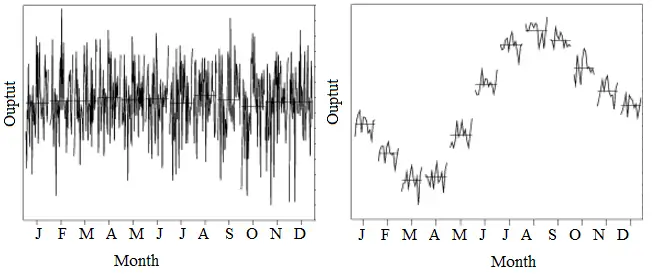
El gráfico de la izquierda es estacionario sin una tendencia evidente, mientras que el gráfico de la derecha muestra estacionalidad y no es estacionario.

Tipos de papelería

Los modelos pueden mostrar diferentes tipos de estacionariedad:

• La estacionariedad estricta significa que la distribución conjunta de cualquier momento de cualquier grado (por ejemplo , valores esperados , varianzas , tercer orden y momentos superiores) dentro del proceso nunca depende del tiempo. En la práctica, esta definición es demasiado estricta para ser utilizada para cualquier modelo de la vida real.
• Las series de estacionariedad de primer orden tienen medias que nunca cambian con el tiempo. Cualquier otra estadística (como la varianza) puede cambiar.
• Las series de tiempo de estacionariedad de segundo orden (también llamada estacionariedad débil) tienen una media constante, una varianza y una autocovarianza que no cambia con el tiempo. Otras estadísticas en el sistema son libres de cambiar con el tiempo. Esta versión restringida de estacionariedad estricta es muy común.
• Los modelos de tendencia estacionaria fluctúan alrededor de una tendencia determinista (la media de la serie). Estas tendencias deterministas pueden ser lineales o cuadráticas, pero la amplitud (altura de una oscilación) de las fluctuaciones no aumenta ni disminuye a lo largo de la serie.
• Los modelos estacionarios en diferencias son modelos que necesitan una o más diferenciaciones para volverse estacionarios (consulte Transformación de modelos a continuación).

Puede ser difícil saber si un modelo está estacionario o no. A diferencia del ejemplo obvio que muestra la estacionalidad anterior, por lo general no se puede saber mirando un gráfico. Si no está seguro acerca de la estacionariedad de un modelo, una prueba de hipótesis puede ayudar. Tiene varias opciones para la prueba, que incluyen:

• Pruebas de raíz unitaria (por ejemplo, prueba de Dickey-Fuller aumentada (ADF) o prueba de Zivot-Andrews),
• Una prueba KPSS (ejecutada como complemento a las pruebas de raíz unitaria).
• Un gráfico de secuencia de ejecución,
• La prueba Priestley-Subba Rao (PSR) o la prueba basada en Wavelet , que son pruebas menos comunes basadas en el análisis de espectro.

¿Por qué es importante la estacionariedad?

La mayoría de los métodos de pronóstico asumen que una distribución tiene estacionariedad. Por ejemplo, la autocovarianza y las autocorrelaciones se basan en el supuesto de estacionariedad. La ausencia de estacionariedad puede causar comportamientos inesperados o extraños, como proporciones t que no siguen una distribución t o valores altos de r cuadrado asignados a variables que no están correlacionadas en absoluto.

Transformando Modelos

La mayoría de los conjuntos de datos de la vida real simplemente no son estacionarios. Para citar a Thomson (1994):

“Sin embargo, la experiencia con datos del mundo real pronto convence de que tanto la estacionariedad como la gaussianidad son cuentos de hadas inventados para la diversión de los estudiantes universitarios”.

Para decirlo de otra manera, si tiene un conjunto de datos de la vida real (y no uno teórico de una clase), necesitará hacerlo estacionario para obtener predicciones útiles de él. A veces, un modelo se puede estacionarizar mediante una transformación matemática (generalmente realizada por software), lo que hace que el modelo sea relativamente fácil de predecir; Tendrá las mismas propiedades estadísticas en una fecha posterior. Luego, las transformaciones matemáticas se invierten para que el nuevo modelo prediga el comportamiento del modelo de serie temporal original. Las transformaciones pueden incluir:

• Diferenciar los datos: los datos diferenciados tienen un punto menos que los datos originales. Por ejemplo, dada una serie Z _t se puede crear una nueva serie Y yo = Z _yo – Z _yo – 1.
• Ajuste una curva a los datos, luego modele los residuos de esa curva.
• Tome el logaritmo o la raíz cuadrada (generalmente funciona para datos con varianza no constante).

Algunos modelos no se pueden transformar de esta manera, como los modelos con estacionalidad . A veces, estos pueden dividirse en piezas más pequeñas (un proceso llamado estratificación ) y transformarse individualmente. Otra forma de lidiar con la estacionalidad es restar el valor medio de la función periódica de los datos.

2. Diferenciación

La diferenciación es donde sus datos tienen un punto de datos menos que el conjunto de datos original; Está restando (o moviendo) un punto, una «diferencia». Por ejemplo, dada una serie Zt, puede crear una nueva serie Yi = Zi – Zi – 1. Además de su uso general en transformaciones, la diferenciación se usa ampliamente en el análisis de series de tiempo .

“Se dice que una serie sin componente determinista que tiene una representación ARMA estacionaria e invertible después de diferenciar d veces está integrada de orden d… (Engle y Granger 1987, p. 252.)”

En cálculo , la diferenciación se utiliza para la diferenciación numérica . La idea general es similar (p. ej., al diferenciar hacia atrás se resta un punto), pero las aplicaciones son diferentes. Si bien la diferenciación en cálculo aún implica «mover» un punto, el movimiento es para que pueda estimar una derivada (es decir, la pendiente ).

Referencias:

Engle, RF y Granger, CWJ (1991) Relaciones económicas a largo plazo: Lecturas sobre cointegración, Oxford University Press.
Priestley, M. & Subba Rao, T. (1969) Una prueba de no estacionariedad de series temporales. Revista de la Real Sociedad Estadística. Serie B (Metodológica), vol. 31, núm. 1, págs. 140-149.
Von Sachs, R. y Neumann, M. (2000). Una prueba de estacionariedad basada en ondículas. Revista de análisis de series temporales. vol. 21, No. 5. Septiembre, pp. 597-613.
Thomson, DJ 1994. Jackknifing espectros de múltiples ventanas. En: Actas de la Conferencia Internacional IEEE sobre Acústica, Habla y Procesamiento de Señales, VI, 73-76.