Contenido de este artículo
Actualizado el 26 de diciembre de 2021, por Luis Benites.
¿Qué es Probabilístico?
Un método o modelo probabilístico se basa en la teoría de la probabilidad o en el hecho de que la aleatoriedad desempeña un papel en la predicción de eventos futuros. Lo opuesto es determinista , que es lo opuesto a aleatorio: nos dice que algo se puede predecir exactamente, sin la complicación adicional de la aleatoriedad.
¿Qué es un modelo probabilístico?
Los modelos probabilísticos incorporan variables aleatorias y distribuciones de probabilidad en el modelo de un evento o fenómeno. Mientras que un modelo determinista da un único resultado posible para un evento, un modelo probabilístico da una distribución de probabilidad como solución. Estos modelos tienen en cuenta el hecho de que rara vez podemos saber todo acerca de una situación. Casi siempre hay un elemento de aleatoriedad a tener en cuenta. Por ejemplo, el seguro de vida se basa en que sabemos con certeza que vamos a morir, pero no sabemos cuándo . Estos modelos pueden ser en parte deterministas y en parte aleatorios o totalmente aleatorios.
Las variables aleatorias de la distribución normal , la distribución binomial y la distribución de Bernoulli forman la base de este tipo de modelado.
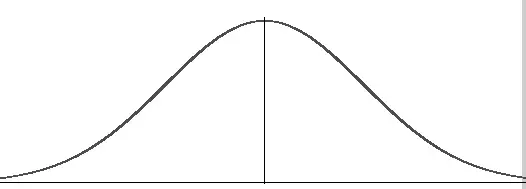
Una curva de distribución normal, a veces llamada curva de campana, es uno de los componentes básicos de un modelo probabilístico.
¿Qué es el Método Probabilístico?
El método probabilístico, introducido por primera vez por Paul Erdős , es una forma de probar la existencia de una estructura con ciertas propiedades en combinatoria . La idea es que cree un espacio de probabilidad y, eligiendo elementos al azar, demuestre que cualquier elemento aleatorio del espacio tiene una probabilidad positiva y las propiedades buscadas. El método se usa ampliamente en una variedad de disciplinas, que incluyen: física estadística, mecánica cuántica e informática teórica.
Referencias :
Alon, Noga; Spencer, Joel H. (2000). El método probabilístico (2ed) . Nueva York: Wiley-Interscience. ISBN 0-471-37046-0.
Billingsley, Patrick, (1995). Probabilidad y medida , tercera edición. Nueva York: Wiley.
Erdös, P. (1959). Gráficos y probabilidad . Canadá. J. Matemáticas. 11 (0): 34–38. doi:10.4153/CJM-1959-003-9. MR 0102081.
Erdős, P. (1961). Gráficas y probabilidad, II . Canadá. J. Matemáticas. 13 (0): 346–352. doi:10.4153/CJM-1961-029-9. MR 0120168.
Humphreys, Paul, (1989). Las posibilidades de explicación: explicaciones causales en las ciencias sociales, médicas y físicas. Princeton: Prensa de la Universidad de Princeton.
