Actualizado por ultima vez el 26 de diciembre de 2021, por Luis Benites.
¿Cuál es la desviación absoluta mediana?
La desviación absoluta mediana (MAD) es una medida robusta de cuán disperso está un conjunto de datos. La varianza y la desviación estándar también son medidas de dispersión , pero se ven más afectadas por valores extremadamente altos o extremadamente bajos y por la no normalidad . Si sus datos son normales , la desviación estándar suele ser la mejor opción para evaluar la dispersión. Sin embargo, si sus datos no son normales, la MAD es una estadística que puede usar en su lugar.
El rango intercuartílico es similar a la MAD y es una estadística más simple. Sin embargo, es menos robusto .
La MAD se define como:
MAD = mediana (| Y i – mediana (Y i |)
La fórmula es una variación de la fórmula de desviación absoluta media (consulte el artículo de desviación absoluta media para obtener más ayuda para resolver la fórmula). Se ve menos afectado por los valores atípicos porque los valores atípicos tienen un efecto menor en la mediana que en la media.
El término desviación absoluta mediana se refiere a una estadística calculada a partir de una muestra. Sin embargo, se puede utilizar para estimar el parámetro de población .
Ejemplo MAD
Ejemplo: Encuentra la MAD del siguiente conjunto de números: 3, 8, 8, 8, 8, 9, 9, 9, 9.
Paso 1: Encuentra la mediana . La mediana de este conjunto de números es 8.
Paso 2: Resta la mediana de cada valor x usando la fórmula |y i – mediana|.
|3 – 8| = 5
|8 – 8| = 0
|8 – 8| = 0
|8 – 8| = 0
|8 – 8| = 0
|9 – 8| = 1
|9 – 8| = 1
|9 – 8| = 1
|9 – 8| = 1
Paso 3: encuentra la mediana de las diferencias absolutas. La mediana de las diferencias (0,0,0,0, 1 ,1,1,1,5) es 1.
Cómo funciona el MAD para diferentes distribuciones
La siguiente imagen (de NIST.gov ) muestra histogramas de 10 000 números aleatorios extraídos de cuatro distribuciones diferentes: una distribución normal , una distribución exponencial doble, una distribución de Cauchy y una distribución de Tukey-Lambda.
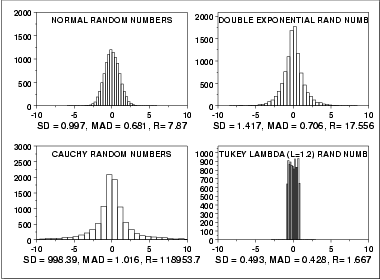
- Normal : la MAD es ligeramente menor que la desviación estándar (SD) ya que pesa ocho veces hacia abajo en las colas. Esta es una razón para no usar la MAD para distribuciones normales.
- Doble exponencial : la SD suele ser demasiado grande, mientras que la MAD es casi igual a la normal.
- Cauchy : el SD es muy grande, mientras que el MAD está encendido, y es un poco más grande de lo normal.
- Distribución Tukey-Lambda : esta distribución tiene colas truncadas (cortadas); SD y MAD son casi iguales.
Notas de robustez
Como se indicó anteriormente, la desviación absoluta mediana es una estadística robusta, incluso para datos extraídos de poblaciones no normales. Sin embargo, robustez puede significar dos cosas diferentes:
- Robustez de validez : los intervalos de confianza para la medida de variación (spread) son del 95 % para cualquier distribución.
- Robustez de la eficiencia : los intervalos de confianza son válidos para las colas no normales.
Si bien la MAD tiene robustez de validez, se ve afectada por colas no normales y, por lo tanto, no tiene robustez de eficiencia.

