Correlación Serial / Autocorrelación: Definición, Pruebas

Actualizado el 2 de octubre de 2021, por Luis Benites.

¿Qué es la Correlación Serial/Autocorrelación?

La correlación serial (también llamada Autocorrelación) es donde los términos de error en una serie de tiempo se transfieren de un período a otro. En otras palabras, el error de un período de tiempo a se correlaciona con el error de un período de tiempo subsiguiente b . Por ejemplo, una subestimación de las ganancias de un trimestre puede resultar en una subestimación de las ganancias de los trimestres subsiguientes. Esto puede resultar en una gran cantidad de problemas , que incluyen:

• Estimaciones de mínimos cuadrados ordinarios ineficientes y cualquier pronóstico basado en esas estimaciones. Un estimador eficiente le brinda la mayor cantidad de información sobre una muestra; los estimadores ineficientes pueden funcionar bien, pero requieren tamaños de muestra mucho más grandes para hacerlo.
• Bondad de ajuste exagerada (para una serie de tiempo con correlación serial positiva y una variable independiente que crece con el tiempo).
• Errores estándar demasiado pequeños (para una serie de tiempo con correlación serial positiva y una variable independiente que crece con el tiempo).
• Estadísticas T que son demasiado grandes.
• Falsos positivos para coeficientes de regresión significativos. En otras palabras, un coeficiente de regresión parece ser estadísticamente significativo cuando no lo es.

Tipos de autocorrelación

La forma más común de autocorrelación es la correlación serial de primer orden , que puede ser positiva o negativa.

• La correlación serial positiva es donde un error positivo en un período se traslada a un error positivo para el período siguiente.
• La correlación serial negativa es donde un error negativo en un período se convierte en un error negativo para el período siguiente.

La correlación serial de segundo orden es donde un error afecta los datos dos períodos de tiempo después. Esto puede suceder cuando sus datos tienen estacionalidad . Los pedidos superiores al segundo orden ocurren, pero son raros.

Prueba de autocorrelación

Puede probar la autocorrelación con:

• Una gráfica de residuos . Trace _t contra t y busque grupos de residuos sucesivos en un lado de la línea cero. También puede intentar agregar una línea Lowess , como en la imagen a continuación.
• Una prueba de Durbin-Watson .
• Una prueba del multiplicador de Lagrange.
• Prueba de caja de Ljung .
• Un correlograma . Un patrón en los resultados es una indicación de autocorrelación. Cualquier valor por encima de cero debe mirarse con sospecha.
• El estadístico I de Moran , que es similar a un coeficiente de correlación .

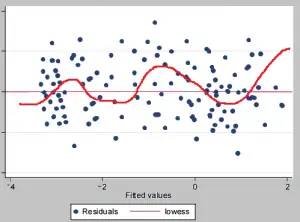
El gráfico de residuos con una línea de Lowess en STATA muestra que la amplitud de los errores parece aumentar con el tiempo (autocorrelación positiva).