Actualizado por ultima vez el 2 de junio de 2022, por Luis Benites.
La prueba de caja de Ljung ( pronunciado Young ) (a veces llamada Box-Pierce modificada, o simplemente prueba de caja ) es una forma de probar la ausencia de autocorrelación serial, hasta un retraso k especificado .
La prueba determina si los errores son iid (es decir, ruido blanco) o si hay algo más detrás de ellos; si las autocorrelaciones para los errores o residuos son distintas de cero o no. Esencialmente, es una prueba de falta de ajuste: si las autocorrelaciones de los residuos son muy pequeñas, decimos que el modelo no muestra una ‘falta de ajuste significativa’.
Hipótesis de la prueba de la caja de Ljung
La hipótesis nula de la prueba de Box Ljung, H 0 , es que nuestro modelo no muestra falta de ajuste (o, en términos simples, el modelo está bien). La hipótesis alternativa , Ha , es simplemente que el modelo muestra una falta de ajuste.
Un valor p significativo en esta prueba rechaza la hipótesis nula de que la serie temporal no está autocorrelacionada.
Cálculo de la estadística de prueba de la caja de Ljung
La mayoría de los paquetes estadísticos pueden ejecutar una prueba de Ljung Box. Por ejemplo, en R , puede implementar la prueba con la función Box.test .
Para ejecutar la prueba de Ljung Box a mano, debe calcular el estadístico Q. Para una serie de tiempo Y de longitud n: = Donde:
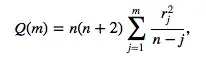
- r j = las autocorrelaciones acumuladas de la muestra,
- m = el tiempo de retraso.
Rechazamos la hipótesis nula y decimos que el modelo muestra falta de ajuste si
![]() Donde:
Donde:
- χ 2 1-α,h = el valor encontrado en la tabla de distribución de chi-cuadrado para el nivel de significación α y h grados de libertad .
Cuando se aplica la prueba de la Caja de Ljung a los residuos de un modelo ARIMA , los grados de libertad h deben ser iguales a mpq, donde p y q son el número de parámetros en el modelo ARIMA(p,q).
Formas alternativas de probar la autocorrelación
La prueba de Durbin-Watson es una forma popular de probar la autocorrelación. Sin embargo, no se puede usar si tiene variables dependientes rezagadas; Si los tiene, use la prueba Breusch-Pagan-Godfrey en su lugar.
La prueba de Ljung Box es una modificación de la prueba Box Pierce . La diferencia está en cómo se calcula la estadística de prueba (Kleiber & Zeileis, 2008). Ambos se aproximan a una estadística de chi-cuadrado, basada en autocorrelaciones hasta el orden p .
- Estadístico de prueba de Box Pierce : n * suma de autocorrelaciones al cuadrado,
- Estadístico de prueba de caja de Ljung : las autocorrelaciones al cuadrado se ponderan en el desfase j por ( n + 2)/( n – j ) ( j = 1…, p ).
Referencias
NIST. Prueba de Box-Ljung. Manual de Estadísticas de Ingeniería 6.4.4.8.1. Recuperado de https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4481.htm el 28 de julio de 2014.
Hyndman, Rob J. Reflexiones sobre la prueba de Ljung-Box. Hyndsight, publicado en línea el 24 de enero de 2014. Recuperado de https://robjhyndman.com/hyndsight/ljung-box-test/ el 28 de julio de 2014.
Kleiber, C. & Zeileis, 2008. Econometría aplicada con R. Springer Science & Business Media, 10 de diciembre de 2008
Estadísticas de PennState. Lección 3.2: Diagnósticos. Stat 510 Análisis de series temporales aplicadas. Recuperado de https://onlinecourses.science.psu.edu/stat510/node/65/ el 28 de julio de 2014.

