Actualizado por ultima vez el 19 de septiembre de 2021, por Luis Benites.
Un fractil es el punto de corte para una determinada fracción de una muestra. Si se conoce su distribución, entonces el fractil es solo el punto de corte donde la distribución alcanza una cierta probabilidad.
En términos visuales, un fractil es el punto en una curva de densidad de probabilidad (PDF) de modo que el área bajo la curva entre ese punto y el origen (es decir, cero) es igual a una fracción específica. Por ejemplo, un fractil de .25 corta el cuarto inferior de una muestra y .5 corta la muestra por la mitad. La siguiente imagen muestra la PDF de una distribución normal junto con las desviaciones estándar (σ) y los fractiles asociados.
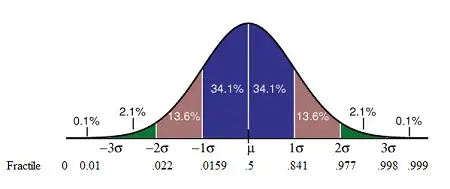
En una distribución normal, un fractil de .5 es igual a la media, μ. En otras palabras, el 50% de la distribución se encuentra por debajo de la media.
Un fractil x p para p mayor que 0.5 se llama fractil superior , y un fractil x p para p menor que 0.5 se llama fractil inferior .
Los fractiles son importantes en las aplicaciones científicas y de ingeniería, y una forma diferente de ellos, los percentiles, vea a continuación, son una de las primeras exposiciones de la vida real que muchos de nosotros tenemos a las estadísticas, ya que nuestros padres buscan los percentiles de crecimiento de nuestros hermanos pequeños y nosotros busque el percentil en el que se encuentran nuestros puntajes SAT.
Cuantiles, Cuartiles, Deciles y Percentiles
La palabra cuantil se usa a veces en lugar de la palabra fractil, y se pueden expresar como cuartiles , deciles o percentiles al expresar el decimal o la fracción α en términos de cuartos, décimos o centésimos respectivamente.
El 1/4-frac x 0.25 es lo mismo que el 1er cuartil. El 1/2-frac es el segundo cuartil y el 3/4-frac es el 3er cuartil.
De la misma manera, el 0.10-frac es el primer decil, el 0.40-frac el cuarto decil, y así sucesivamente.
El frac 0,01 es el primer percentil, el frac 0,23 el percentil 23 y el frac 0,99 el percentil 99.
Terminología
Más precisamente , para una distribución continua de una variable aleatoria podemos definir α fractil (x α ) como ese punto en la distribución tal que la variable X tiene una probabilidad α de ser menor o igual que el punto.
Simbólicamente, podemos definir el fractil x p escribiendo
P(X ≤ x p )= Φ (x p ) = p .
Aquí φ (x) es la función de distribución de su variable aleatoria X. Mirando el fractil de 0.8441 en la imagen de arriba, P(X ≤ (μ + σ) )= φ (μ + σ)) = 0.8441, entonces x p = μ + σ. Si su distribución tiene una media de 6 y una desviación estándar de 2, el fractil de 0.8441 será 8 y el fractil de 0.5 = 6.
Cálculos
Un fractil es solo un punto de corte para una cierta probabilidad, por lo que si se conoce su distribución, puede buscarla en la tabla correspondiente. Por ejemplo, la tabla z muestra estos puntos de corte (x p ) para la distribución normal.
Puede calcular el x p de su variable aleatoria no estándar X desde el fractil up usando la variable estandarizada U con la siguiente fórmula:
![]() .
.
Donde:
- V es el coeficiente de variación de su variable X.
- μ es la media
- σ es la desviación estándar
- up es el fractil de la variable normal estandarizada correspondiente a la probabilidad p . Por ejemplo, u 0.1 corresponde a p = .1
Para encontrarlo , consulte una tabla para la distribución específica con la que está trabajando. Por ejemplo, la siguiente tabla muestra una variable aleatoria estandarizada con una distribución normal (de Introducción a la probabilidad y estadística para ingenieros de Milan Holický ). Por ejemplo, suponga que desea calcular el valor de x p para p = 0,10 donde el coeficiente de variabilidad es 0,3 y la media 5. u p es 1,282, por lo que x p será 5(1 + 1,282 · 0,3) o 6,923.

Calcular fractiles para variables cuando no conoce la distribución subyacente puede ser complicado. Hay tres métodos disponibles: método de cobertura clásico, método de predicción y un enfoque bayesiano. Estas herramientas avanzadas suelen ser utilizadas por ingenieros y se pueden encontrar en las publicaciones pertinentes de la Organización Internacional de Normalización (ISO). Por ejemplo, la cobertura clásica se describe en ISO 12491 .
- El método de cobertura clásico obtiene valores dentro de un cierto intervalo de confianza, en lugar de una cifra exacta. Aunque este método puede funcionar con tamaños de muestra muy pequeños, la asimetría debe conocerse por experiencia previa.
- El método de predicción, los límites de predicción se utilizan como una restricción para nuevos valores.
- El enfoque bayesiano utiliza conocimientos previos para distribuciones de variables aleatorias.
Se pueden encontrar más detalles sobre estos tres métodos en Introducción a la probabilidad y estadística para ingenieros de Holický.
Referencias
Agarwal, B. Estadísticas básicas . Anshan Publishers, 2012.
Holicky, M. Introducción a la probabilidad y estadística para ingenieros. Springer Science & Business Media, 2013.
Madsen B. Estadísticas para no estadísticos . Springer Science & Business Media. 2011.

